题目内容
16.计算:①$\sqrt{\frac{25}{9}}-{({\frac{8}{27}})^{\frac{1}{3}}}-{(π+e)^0}+{({\frac{1}{4}})^{-\frac{1}{2}}}$
②$2lg5+lg4+ln\sqrt{e}+{log_{25}}5$.
分析 ①②指数幂与对数的运算性质即可得出.
解答 解:①原式=$\frac{5}{3}-(\frac{2}{3})^{3×\frac{1}{3}}$-1+$(\frac{1}{2})^{2×(-\frac{1}{2})}$
=$\frac{5}{3}$-$\frac{2}{3}$-1+2
=2.
②原式=lg(52×4)+$\frac{1}{2}$+$\frac{lg5}{2lg5}$
=2+$\frac{1}{2}$+$\frac{1}{2}$
=3.
点评 本题考查了指数幂与对数的运算性质,考查了计算能力,属于基础题.

练习册系列答案
相关题目
9.已知变量x、y满足约束条件$\left\{{\begin{array}{l}x+y≤1\\ x-y≤1\\ x+1≥0\end{array}}\right.$,则z=x-2y的最大值为( )
| A. | 3 | B. | 1 | C. | -5 | D. | -6 |
4.已知f(x)是偶函数,且在[0,1]上是增函数,则f(0.5)、f(-1)、f(0)的大小关系是( )
| A. | f(0.5)<f(0)<f(-1) | B. | f(-1)<f(0.5)<f(0) | C. | f(0)<f(0.5)<f(-1) | D. | f(-1)<f(0)<f(0.5) |
5.下列关系式中表述正确的是( )
| A. | 0∈{(0,0)} | B. | 0∈∅ | C. | 0∈N | D. | {0}∈{x|x2=0} |
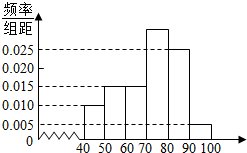 某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如如图所示的部分频率分布直方图,请观察图形信息,回答下列问题: