题目内容
f(x)是偶函数,当x<0时,f(x)=x(x+1),求的解析式,画出函数图象,并写出单调区间.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)根据偶函数的定义求解f(x)=
,(2)画出图象,据图写出单调区间.
|
解答:
解:∵f(x)是偶函数,
∴f(-x)=f(x),
∵当x<0时,f(x)=x(x+1),
∴设x>0,则-x<0,
∴f(x)=f(-x)=-x(1-x)=x(x-1),(x>0)
∴f(x)=
,
(2)(
,+∞)(-
,0)单调递增,(-∞,-
)(
,0)单调递减.

∴f(-x)=f(x),
∵当x<0时,f(x)=x(x+1),
∴设x>0,则-x<0,
∴f(x)=f(-x)=-x(1-x)=x(x-1),(x>0)
∴f(x)=
|
(2)(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

点评:本题考查了函数的性质,图象,运用图象解决问题,属于中档题.

练习册系列答案
相关题目
当0<x<1,函数y=x(1-x)的最大值为( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
将一枚质地均匀的硬币连抛三次,则“至少出现一次正面向上”的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
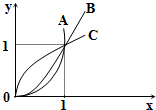 已知幂函数①y=x
已知幂函数①y=x | 1 |
| 2 |
| A、①②③ | B、③①② |
| C、③②① | D、①③② |
设集合M={x|x-m<0},N={y|y=2x-1,x∈R},若M∩N=∅,则m的范围是( )
| A、m≥-1 | B、m>-1 |
| C、m≤-1 | D、m<-1 |