题目内容
8.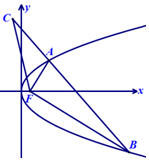 如图,A,B为抛物线y2=4x上的两点,F为抛物线的焦点且FA⊥FB,C为直线AB上一点且横坐标为-1,连结FC.若|BF|=3|AF|,则tanC=$\frac{1}{2}$.
如图,A,B为抛物线y2=4x上的两点,F为抛物线的焦点且FA⊥FB,C为直线AB上一点且横坐标为-1,连结FC.若|BF|=3|AF|,则tanC=$\frac{1}{2}$.
分析 如图所示,设|AF|=a,|BF|=3a,可得|AB|=$\sqrt{10}$a,做FH⊥AB于H,求出|FH|,|CH|,即可得出结论.
解答  解:如图所示,设|AF|=a,|BF|=3a,可得|AB|=$\sqrt{10}$a,
解:如图所示,设|AF|=a,|BF|=3a,可得|AB|=$\sqrt{10}$a,
作AA′⊥l(l为抛物线的准线),则|AA′|=|AF|=a,|BB′|=|BF|=3a,
|A′B′|=|AD|=$\sqrt{6}$a.△CA′A∽△CB′B,可得$\frac{AA′}{BB′}$=$\frac{1}{3}$,
CA=$\frac{1}{2}$AB=$\frac{\sqrt{10}}{2}$a,
做FH⊥AB于H,△ABF三边长为a,3a,$\sqrt{10}$a,
∴|FH|=$\frac{3\sqrt{10}}{10}$a,|AH|=$\frac{\sqrt{10}}{10}$a,
∴tanC=$\frac{|FH|}{|CH|}$=$\frac{\frac{3\sqrt{10}}{10}a}{\frac{\sqrt{10}}{2}a+\frac{\sqrt{10}}{10}a}$=$\frac{1}{2}$,
故答案为$\frac{1}{2}$.
点评 本题考查了抛物线的定义,考查三角形相似的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.设x∈Z,A={奇数},B={偶数},若命题p:?x∈A,2x∈B,则其否定为( )
| A. | ?x∈A,2x∉B | B. | ?x∉A,2x∉B | C. | ?x∉A,2x∈B | D. | ?x∈A,2x∉B |
16.心理学家分析发现“喜欢空间现象”与“性别”有关,某数学兴趣小组为了验证此结论,从全体组员中按层抽样的方法抽取50名同学(男生30人,女生20人),给每位同学立体几何体,代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如表:(单位:人)
(1)能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关?
(2)经统计得,选择做立体几何题的学生正答率为$\frac{4}{5}$,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
附表及公式:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 立体几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
(2)经统计得,选择做立体几何题的学生正答率为$\frac{4}{5}$,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
附表及公式:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
13.设集合A={1,2,3},B={1,2,3},分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线x+y=n上”为事件Cn(2≤n≤6,n∈N),若事件Cn的概率最大,则n的所有可能值为( )
| A. | 4 | B. | 2和6 | C. | 3和5 | D. | 3 |
20.设函数f(x)=-2x,g(x)=lg(ax2-2x+1),若对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )
| A. | (-1,0) | B. | (0,1) | C. | (-∞,1] | D. | [1,+∞) |
17.若$tan({α+\frac{π}{4}})=2$,则$\frac{sinα-cosα}{sinα+cosα}$=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | $-\frac{1}{2}$ |
18.阅读如图所示的程序框图,运行相应的程序,输出的S的值等于( )


| A. | 15 | B. | 16 | C. | 17 | D. | 18 |