题目内容
16.心理学家分析发现“喜欢空间现象”与“性别”有关,某数学兴趣小组为了验证此结论,从全体组员中按层抽样的方法抽取50名同学(男生30人,女生20人),给每位同学立体几何体,代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如表:(单位:人)| 立体几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
(2)经统计得,选择做立体几何题的学生正答率为$\frac{4}{5}$,且答对的学生中男生人数是女生人数的5倍,现从选择做立体几何题且答错的学生中任意抽取两人对他们的答题情况进行研究,求恰好抽到男女生各一人的概率.
附表及公式:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)由表中数据计算K2,对照临界值表即可得出结论;
(2)计算对应的基本事件数,求出对应的概率值.
解答 解:(1)由表中数据,计算
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$=$\frac{50{×(22×12-8×8)}^{2}}{30×20×30×20}$=$\frac{50}{9}$>5.024,
故有97.5%以上的把握认为“喜欢空间想象”与“性别”有关;
(2)由题知选做立体几何题且答对的共24人,其中男生20人、女生4人,
故答错的共6人,其中男生2人、女生4人,
则从6人中任取2人共有15种不同结果,
其中恰好抽到一男一女的结果有8种,
所以P=$\frac{8}{15}$.
点评 本题考查了独立性检验的应用问题,也考查了古典概型的概率计算问题,是基础题目.

练习册系列答案
相关题目
17.曲线y=2lnx上的点到直线2x-y+3=0的最短距离为( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | 2 |
11.执行如图所示的程序,则输入的i的值为( )


| A. | -1 | B. | 0 | C. | -1或2 | D. | 2 |
6.已知函数$f(x)={log_2}x,x∈[\frac{1}{2},4]$,在区间$[\frac{1}{2},4]$上任取一点x0,则f(x0)≤0的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{7}$ |
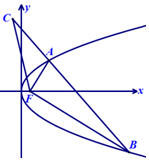 如图,A,B为抛物线y2=4x上的两点,F为抛物线的焦点且FA⊥FB,C为直线AB上一点且横坐标为-1,连结FC.若|BF|=3|AF|,则tanC=$\frac{1}{2}$.
如图,A,B为抛物线y2=4x上的两点,F为抛物线的焦点且FA⊥FB,C为直线AB上一点且横坐标为-1,连结FC.若|BF|=3|AF|,则tanC=$\frac{1}{2}$.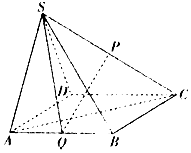 如图,在四棱锥S-ABCD中,底面ABCD为正方形,△SAD是正三角形,P,Q分别是棱SC,AB的中点,且平面SAD⊥平面ABCD.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,△SAD是正三角形,P,Q分别是棱SC,AB的中点,且平面SAD⊥平面ABCD.