题目内容
20.设函数f(x)=-2x,g(x)=lg(ax2-2x+1),若对任意x1∈R,都存在x2∈R,使f(x1)=g(x2),则实数a的取值范围为( )| A. | (-1,0) | B. | (0,1) | C. | (-∞,1] | D. | [1,+∞) |
分析 由题意求出f(x)的值域,再把对任意x1∈R,都存在x2∈R,使f(x1)=g(x2)转化为函数g(x)的值域包含f(x)的值域,进一步转化为关于a的不等式求解.
解答 解:∵f(x)=-2x<0,
∴?x1∈R,f(x)=-2x∈(-∞,0),
∵?x2∈R,使f(x1)=g(x2),
∴g(x)=lg(ax2-2x+1)的值域包含(-∞,0),
设y=ax2-2x+1的值域为B,
则(0,1]⊆B.
由题意当a=0时,上式成立.
当a>0时,△=4-4a≥0,解得0<a≤1.
当a<0时,ymax=$\frac{4a-4}{4a}$≥1,即$-\frac{1}{a}$≥0恒成立.
综上,a≤1.
∴实数a的取值范围是(-∞,1].
故选:C.
点评 本题考查函数的值域,体现了数学转化思想方法,正确理解题意是解答该题的关键,是中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
11.执行如图所示的程序,则输入的i的值为( )


| A. | -1 | B. | 0 | C. | -1或2 | D. | 2 |
15.经过A(0,-1),B(2,3)的直线的斜率等于( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
9. 某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.图1是甲流水线样本的频率分布直方图,表1是乙流水线样本频数分布表.
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.图1是甲流水线样本的频率分布直方图,表1是乙流水线样本频数分布表.
表1:(乙流水线样本频数分布表)
(Ⅰ)若以频率作为概率,试估计从甲流水线上任取5件产品,求其中合格品的件数X的数学期望; (Ⅱ)从乙流水线样本的不合格品中任意取x2+y2=2件,求其中超过合格品重量的件数l:y=kx-2的分布列;(Ⅲ)由以上统计数据完成下面$\frac{π}{2}$列联表,并回答有多大的把握认为“产品的包装质量与两条资动包装流水线的选择有关”.
附:下面的临界值表供参考:
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
 某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.图1是甲流水线样本的频率分布直方图,表1是乙流水线样本频数分布表.
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.图1是甲流水线样本的频率分布直方图,表1是乙流水线样本频数分布表.表1:(乙流水线样本频数分布表)
| 产品重量(克) | 频数 |
| (490,495] | 6 |
| (495,500] | 8 |
| (500,505] | 14 |
| (505,510] | 8 |
| (510,515] | 4 |
| 甲流水线 | 乙流水线 | 合计 | |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合 计 | n= |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
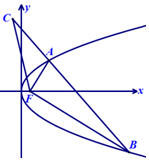 如图,A,B为抛物线y2=4x上的两点,F为抛物线的焦点且FA⊥FB,C为直线AB上一点且横坐标为-1,连结FC.若|BF|=3|AF|,则tanC=$\frac{1}{2}$.
如图,A,B为抛物线y2=4x上的两点,F为抛物线的焦点且FA⊥FB,C为直线AB上一点且横坐标为-1,连结FC.若|BF|=3|AF|,则tanC=$\frac{1}{2}$.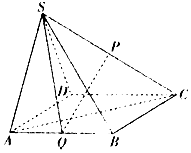 如图,在四棱锥S-ABCD中,底面ABCD为正方形,△SAD是正三角形,P,Q分别是棱SC,AB的中点,且平面SAD⊥平面ABCD.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,△SAD是正三角形,P,Q分别是棱SC,AB的中点,且平面SAD⊥平面ABCD.