题目内容
6．已知α∈（0，$\frac{π}{2}$），β∈（0，$\frac{π}{2}$），则2α-$\frac{β}{3}$的取值范围是（-$\frac{π}{6}$，π）．分析 首先，确定2α与-$\frac{β}{3}$的范围，然后求解2α-$\frac{1}{3}$β的范围．
解答 解：∵0＜α＜$\frac{π}{2}$，0＜β＜$\frac{π}{2}$，
∴0＜2α＜π，-$\frac{π}{6}$＜-$\frac{1}{3}$β＜0，
∴-$\frac{π}{6}$＜2α-$\frac{β}{3}$＜π，
故答案为：（-$\frac{π}{6}$，π）．
点评 本题重点考查了不等式的基本性质，属于基础题，解题关键是灵活运用不等式的基本性质求解．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
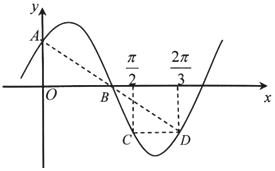如图，已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π），点A，B分别是f（x）的图象与y轴、x轴的交点，C，D分别是f（x）的图象上横坐标为$\frac{π}{2}$、$\frac{2π}{3}$的两点，CD∥x轴，A，B，D共线．