题目内容
如图，在正方体ABCD-A1B1C1D1中，P为AB的中点，求直线A1P与平面D1ABC1所成角的正切值是 ．
考点：直线与平面所成的角
专题：空间角
分析：首先根据面面垂直转化成线面垂直，在转化成线线垂直，进一步求出线面的夹角，在通过解直角三角形求得结果．
解答：
解：连接AD1和A1D交于O，并连接PO，A1P
所以：A1O⊥平面D1ABC1，PO?平面D1ABC1
所以：A1O⊥PO
直线A1P与平面D1ABC1所成角即：∠A1PO
设正方体的棱成为2，
则解得：A1O=
，PO=
在Rt△A1PO中，tan∠A1PO=
=
=
故答案为：
所以：A1O⊥平面D1ABC1，PO?平面D1ABC1
所以：A1O⊥PO
直线A1P与平面D1ABC1所成角即：∠A1PO
设正方体的棱成为2，
则解得：A1O=
| 2 |
| 3 |
在Rt△A1PO中，tan∠A1PO=
| A1O |
| PO |
| ||
|
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题考查的知识要点：线面垂直与线线垂直的转化，直线与平面所成的角．属于基础题型．
练习册系列答案
相关题目
已知集合A={x∈R|-3≤x≤4}，B={x∈R|log2x≥1}，则A∩B=（ ）
| A、[4，+∞） |
| B、（4，+∞） |
| C、[2，4） |
| D、[2，4] |
如图，在四边形ABCD中，AB=CD，CB=CD，AC与BD相交于O点，OC=OA，若E是CD上任意一点，连接BE交AC于点F，连接DF．
如图，PA与⊙O切于点A，过点P的割线与弦AC交于B，与⊙O交于D、E，且PA=PB=BC，若PD=4，DE=21，则AB=圆锥侧面展开图是半径为a的半圆，这个圆锥的高是（ ）
| A、a | ||||
B、
| ||||
C、
| ||||
D、
|
如图，点P为⊙O的弦AB上的一点，连接OP，过点P作PC⊥OP，PC为⊙O于点C，若OC=4，∠POC=60°，则PA•PB=已知集合P={x|0≤x≤4}，集合N={y|0≤y≤2}，下列从P到Q的各对应关系f不是函数的是（ ）
A、f：x→y=
| ||
B、f：x→y=
| ||
C、f：x→y=
| ||
D、f：x→y=
|
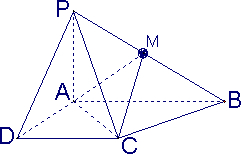已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=