题目内容
15.已知函数f(x)=sin(2x+$\frac{π}{3}$),则f(x)满足( )| A. | 最大值为2 | B. | 图象关于点($\frac{π}{3}$,0)对称 | ||
| C. | 图象关于直线x=-$\frac{π}{3}$对称 | D. | 在(0,$\frac{π}{4}$)上为增函数 |
分析 利用正弦函数的图象和性质,得出结论.
解答 解:∵函数f(x)=sin(2x+$\frac{π}{3}$),故它的最大值为1,故排除A;
当x=$\frac{π}{3}$时,f(x)=0,故它的图象关于点($\frac{π}{3}$,0)对称,故B满足条件;
当x=-$\frac{π}{3}$时,f(x)=-$\frac{\sqrt{3}}{2}$,不是最值,故它的图象不关于x=-$\frac{π}{3}$对称,故C满足条件;
在(0,$\frac{π}{4}$)上,2x+$\frac{π}{3}$∈($\frac{π}{3}$,$\frac{5π}{6}$),函数f(x)不是单调函数,故排除D,
故选:B.
点评 本题主要考查正弦函数的图象和性质,属于基础题.

练习册系列答案
相关题目
20.若函数f(x)=2sin(2x+φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{6}$个单位后经过点($\frac{π}{12}$,-$\sqrt{2}$),则φ等于( )
| A. | -$\frac{π}{12}$ | B. | -$\frac{π}{6}$ | C. | 0 | D. | $\frac{π}{6}$ |
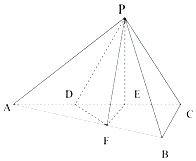 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.