题目内容
设函数f（x）=2cos（ωx+φ）对任意的x∈R，都有f（
+x）=f（
-x），若设函数g（x）=3sin（ωx+φ）-1，则g（
）的值时（ ）
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| A、2 | ||
| B、-4或2 | ||
C、
| ||
| D、-1 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：先根据f（
+x）=f（
-x），确定x=
是函数f（x）的对称轴，再由正余弦函数在其对称轴上取最值得到
ω+φ=
，（k∈Z），然后将x=
代入函数g（x）即可得到答案．
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
解答：
解：函数f（x）=sin（ωx+φ），若对任意的x∈R都有f（
+x）=f（
-x），所以函数的一条对称轴方程为x=
，且x=
时函数f（x）过最高点或最低点．
∴sin（
ω+φ）=±1，∴
ω+φ=
+kπ，（k∈Z）．
g（
）=3cos（
ω+φ）-1=3cos（
+kπ）-1=-1．
故选：D
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴sin（
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
g（
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
故选：D
点评：本题主要考查三角函数的对称轴的问题．注意正余弦函数在其对称轴上取最值．
练习册系列答案
相关题目
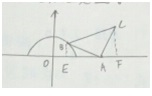已知B是x2+y2=1（y∈[0，1]）上一动点，A（2，0）△ABC是以A为直角顶点的等腰三角形，且A，B，C按顺时针方向排列，则动点C的轨迹方程是已知定义在[1-2a，2-a]上的偶函数f（x），当x≥0时，f（x）=x+ex，若f（t）＜f（2t-1）．则t的取值范围是（ ）
| A、[-1，1] | ||
| B、[0，1] | ||
C、[
| ||
D、[0，
|
矩形ABCD中，AB=3cm，BC=6cm，点P从B出发以3cm/s的速度逆时针匀速运动一周回到B，同时直线l从CD出发以1cm/s的速度沿C到B方向匀速运动，当点P停止运动，设运动时间为t（s）．