Question

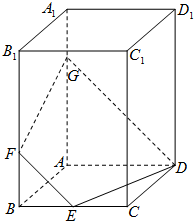如图，ABCD-A₁B₁C₁D₁是长方体，AB=BC=2，E、F分别是棱BC、BB₁上一点，BE=BF=1，经过D、E、F三点的平面与棱AA₁相交于G．
（1）求AG；
（2）求二面角A-FG-D的余弦值．

Answer 1

考点：与二面角有关的立体几何综合题

专题：空间位置关系与距离,空间角

分析：（1）由已知条件推导出面BCC₁B₁∥面ADD₁A₁，EF∥DG，从而得到∠BEF=∠ADG，由此能求出AG．
（2）几何法：在平面ABB₁A₁内作AH⊥FG，垂足为H，连接DH，则∠AHD是二面角A-FG-D的平面角，由此能求出二面角A-FG-D的余弦值．
（2）向量法二：以B为原点，BC、BA、BB₁所在直线分别为x轴、y轴、z轴，建立空间直角坐标系，利用向量法能求出二面角A-FG-D的余弦值．

解答： 解：（1）∵ABCD-A₁B₁C₁D₁是长方体，∴面BCC₁B₁∥面ADD₁A₁…（1分）
∵DEFG在同一平面上，∴EF∥DG…（2分），
∴∠BEF=∠ADG…（3分）
由已知得△BEF和△ADG都是等腰直角三角形，
∴AG=AD=2．…（4分）
（2）几何法：
在平面ABB₁A₁内作AH⊥FG，垂足为H，
连接DH…（5分）
∵AD⊥面ABB₁A₁，∴AD⊥FG…（6分）
∵AD∩AH=A，∴AD⊥面ADH…（7分）
∴FG⊥AH，
∴∠AHD是二面角A-FG-D的平面角…（8分）
在△AFG中，AF=FG=

5

，AG=2…（9分）
由余弦定理得cos∠AFG=

3

5

…（11分）
∴sin∠AFG=

4

5

，
AH=AF×sin∠AFG=

4 5

5

…（12分）
∴DH=

AH2+AD2

=

6 5

5

…（13分），
cos∠AHD=

AH

DH

=

2

3

，
∴二面角A-FG-D的余弦值为

2

3

．…（14分）
（2）向量法：
以B为原点，BC、BA、BB₁所在直线分别为x轴、y轴、z轴，
建立空间直角坐标系…（5分），
平面AFG的一个法向量为

n1

=(1，0，0)…（6分）
由题意知D（2，2，0），E（1，0，0），F（0，0，1），…（7分）
设平面DFG即平面DEF的一个法向量为

n2

=(a，b，c)，
则

n2 • DE =0 n2 • EF =0

…（9分），
即

a+2b=0 -a+c=0

…（11分），a=c=-2b，不妨取

n2

=(2，-1，2)…（12分）
∴二面角A-FG-D的余弦值cosθ=

| n1 • n2 |

| n1 |•| n2 |

=

2

3

…（14分）

点评：本题考查线段长的求法，考查二面角的余弦值的求法，解题时要认真审题，注意空间思维能力的培养．