题目内容
复数z=
在复平面内对应的点位于( )
| 2 |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:直接利用复数代数形式的乘除运算化简,求出复数所对应点的坐标得答案.
解答:
解:由z=
=
=
=1-i,
得复数z=
在复平面内对应的点的坐标为(1,-1),位于第四象限.
故选:D.
| 2 |
| 1+i |
| 2(1-i) |
| (1+i)(1-i) |
| 2(1-i) |
| 2 |
得复数z=
| 2 |
| 1+i |
故选:D.
点评:本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
“m<1”是“函数f(x)=x2+x+m有零点”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知α、β是两个不同的平面,m、n是平面α及平面β之外的两条不同直线,给出四个论断:①m∥n,②α∥β,③m⊥α,④n⊥β.以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题: .
已知集合A={y∈Z|y=log2x,
<x≤8},B={x|
≥0},则A∩B等于( )
| 1 |
| 2 |
| x |
| x-2 |
| A、{0,3} |
| B、(-1,3] |
| C、{-1,0,1,2} |
| D、[-1,3) |
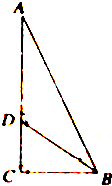
如图,已知直角三角形ACB中,∠C=90°,D为AC上一点,且
=2
,∠ABD=30°,则cos∠ADB=( )
| AD |
| DC |

A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
