题目内容
直线L与双曲线
-
=1相交于A，B两点，点N满足
=
，且点N的坐标是（-12，-15），则直线L必过双曲线的（ ）
| x2 |
| 4 |
| y2 |
| 5 |
| AN |
| NB |
| A、左顶点 | B、右顶点 |
| C、左焦点 | D、右焦点 |
考点：双曲线的简单性质
专题：计算题,平面向量及应用,直线与圆,圆锥曲线的定义、性质与方程
分析：判断N为AB的中点，设A（x1，y1），B（x2，y2），运用中点坐标公式，及点在双曲线上，得到方程，再作差运用平方差公式和斜率公式，求得AB的斜率，进而得到直线AB的方程，令y=0，解得x，即可判断．
解答：
解：点N满足
=
，
则N为AB的中点，
设A（x1，y1），B（x2，y2），
则x1+x2=-24，y1+y2=-30，
-
=1，
-
=1，
两式相减得，
=
，
即有kAB=
=
=1，
则有AB：y+15=x+12，
即有y=x-3．
令y=0，则x=3．
则经过右焦点F（3，0）．
故选D．
| AN |
| NB |
则N为AB的中点，
设A（x1，y1），B（x2，y2），
则x1+x2=-24，y1+y2=-30，
| x12 |
| 4 |
| y12 |
| 5 |
| x22 |
| 4 |
| y22 |
| 5 |
两式相减得，
| (x1-x2)(x1+x2) |
| 4 |
| (y1-y2)(y1+y2) |
| 5 |
即有kAB=
| y1-y2 |
| x1-x2 |
| 5×(-24) |
| 4×(-30) |
则有AB：y+15=x+12，
即有y=x-3．
令y=0，则x=3．
则经过右焦点F（3，0）．
故选D．
点评：本题考查双曲线的方程和性质，考查点差法解决中点弦问题，考查运算能力，属于中档题．
练习册系列答案
相关题目
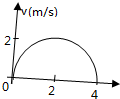如图所示，一个物体在4s内的速度图象恰好时一个半圆，以下关于物体的运动的说法正确的是（ ）| A、物体前2s作匀加速直线运动，后2s作匀减速直线运动 |
| B、物体在前2s作加速度越来越小的加速运动，后2s作加速度越来越大的减速运动 |
| C、物体在4s内的位移大小是2π（m） |
| D、物体在4s内的位移大小无法确定 |