题目内容
6.已知函数f(x)=axlnx(a≠0,a∈R).(1)若函数f(x)有极小值-$\frac{1}{e}$,求f(x)的单调函数;
(2)证明:当a>0时,f(x)≥a(x-1);
(3)当x∈(1,e)是,不等式$\frac{x-1}{a}$<lnx恒成立,求实数a的取值范围.
分析 (1)求函数的导数,根据函数的极小值确定a的取值范围,即可得到结论.
(2)根据不等式的关系,构造函数,求函数的导数,利用导数和极值之间的关系进行证明即可.
(3)利用参数分离法转化求函数的最值即可得到结论.
解答 解:(1)函数f(x的定义域为(0,+∞).
∵f′(x)=a(lnx+1),
∴f′(x)=0,解得x=$\frac{1}{e}$.
①当a>0时,随着x变化时,f(x)和f′(x)的变化情况如下:
| x | (0,$\frac{1}{e}$) | $\frac{1}{e}$ | ($\frac{1}{e}$,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↘ | ↗ |
即当x=$\frac{1}{e}$时,函数取得极小值f($\frac{1}{e}$)=$\frac{1}{e}$•aln$\frac{1}{e}$=-$\frac{a}{e}$,
若函数f(x)有极小值-$\frac{1}{e}$,∴此时-$\frac{a}{e}$=-$\frac{1}{e}$,得a=1.
②当a<0时,随着x变化时,f(x)和f′(x)的变化情况如下:
| x | (0,$\frac{1}{e}$) | $\frac{1}{e}$ | ($\frac{1}{e}$,+∞) |
| f′(x) | + | 0 | - |
| f(x) | ↗ | ↘ |
即当x=$\frac{1}{e}$时,函数取得极大值f($\frac{1}{e}$)=$\frac{1}{e}$•aln$\frac{1}{e}$=-$\frac{a}{e}$,不满足条件.
故a=1时,函数f(x)在(0,$\frac{1}{e}$)上单调递减,在($\frac{1}{e}$,+∞)上单调递增.
(2)当a>0时,若f(x)≥a(x-1);
则等价为axlnx≥a(x-1),即xlnx≥x-1,
即xlnx-x+1≥0,
设F(x)=xlnx-x+1,
则F′(x)=lnx+1-1=lnx,
当x>1时,F′(x)>0,当0<x<1时,F′(x)<0,
即当x=1时,函数,F(x)=xlnx-x+1极小值,同时也是最小值,
此时F(1)=ln1-1+1=0,
即F(x)≥F(1)=0,
即xlnx-x+1≥0成立,即当a>0时,f(x)≥a(x-1)成立;
(3)a>0时,x∈(1,e),0<lnx<1,不等式$\frac{x-1}{a}$<lnx恒成立,等价于a>$\frac{x-1}{lnx}$恒成立,
令g(x)=$\frac{x-1}{lnx}$,g′(x)=$\frac{lnx+\frac{1}{x}-1}{{ln}^{2}x}$,
令h(x)=lnx+$\frac{1}{x}$-1,h′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$>0,x∈(1,e),
∴h(x)在(1,e)递增,hmin(x)>h(1)=0,
∴g′(x)>0在(1,e)恒成立,
∴g(x)max<g(e)=e-1,
∴a≥e-1,
a<0时,a<$\frac{x-1}{lnx}$,∵g(x)=$\frac{x-1}{lnx}$,x∈(1,e),
∵g(x)=$\frac{x-1}{lnx}$>0,恒成立,
∴不等式a<$\frac{x-1}{lnx}$,恒成立,即此时a<0成立,
综上,a≥e-1或a<0.
点评 本题主要考查导数的综合应用,求函数的导数,利用函数单调性,极值和最值与导数之间的关系是解决本题的关键.综合性较强,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.在同一个平面直角坐标系中,函数y=sin($\frac{x}{2}$+$\frac{3π}{2}$)(x∈[0,2π])的图象和直线y=$\frac{1}{2}$的交点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
16.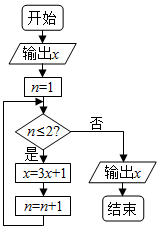 从1,2,3,4,5,6,7,8中随机取出一个数为x,执行如图所示的程序框图,则输出的x不小于40的概率为( )
从1,2,3,4,5,6,7,8中随机取出一个数为x,执行如图所示的程序框图,则输出的x不小于40的概率为( )
 从1,2,3,4,5,6,7,8中随机取出一个数为x,执行如图所示的程序框图,则输出的x不小于40的概率为( )
从1,2,3,4,5,6,7,8中随机取出一个数为x,执行如图所示的程序框图,则输出的x不小于40的概率为( )| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{1}{2}$ |
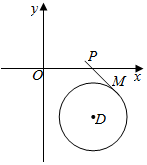 如图,已知圆D:x2+y2-4x+4y+6=0,若P为圆D外一动点,过P向圆D作切线PM,M为切点,设|PM|=2,求动点P的轨迹方程.
如图,已知圆D:x2+y2-4x+4y+6=0,若P为圆D外一动点,过P向圆D作切线PM,M为切点,设|PM|=2,求动点P的轨迹方程.