题目内容
18.设P1P2P3…Pn是圆的内接正n边形,O为圆心,求证:$\overrightarrow{O{P}_{1}}$$+\overrightarrow{O{P}_{2}}$$+\overrightarrow{O{P}_{3}}$+…+$\overrightarrow{O{P}_{n}}$=$\overrightarrow{0}$.分析 分类讨论,从而分偶数与奇数进行讨论,从而证明.
解答 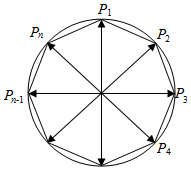 证明:①当n为偶数时,作图如右图,
证明:①当n为偶数时,作图如右图,
故$\overrightarrow{O{P}_{1}}$+$\overrightarrow{O{P}_{\frac{n}{2}+1}}$=$\overrightarrow{0}$,
$\overrightarrow{O{P}_{2}}$+$\overrightarrow{O{P}_{\frac{n}{2}+2}}$=$\overrightarrow{0}$,
…,
$\overrightarrow{O{P}_{\frac{n}{2}}}$+$\overrightarrow{O{P}_{n}}$=$\overrightarrow{0}$,
故$\overrightarrow{O{P}_{1}}$$+\overrightarrow{O{P}_{2}}$$+\overrightarrow{O{P}_{3}}$+…+$\overrightarrow{O{P}_{n}}$=$\overrightarrow{0}$;
②当n为奇数时,作图如右图,
取各段弧的中点,
构造正2n边形,由①知,
$\overrightarrow{O{P}_{1}}$$+\overrightarrow{O{P}_{2}}$$+\overrightarrow{O{P}_{3}}$+…+$\overrightarrow{O{P}_{n}}$+$\overrightarrow{O{Q}_{1}}$+$\overrightarrow{O{Q}_{2}}$+…+$\overrightarrow{O{Q}_{n}}$=$\overrightarrow{0}$;
又∵$\overrightarrow{O{P}_{1}}$$+\overrightarrow{O{P}_{2}}$$+\overrightarrow{O{P}_{3}}$+…+$\overrightarrow{O{P}_{n}}$=$\overrightarrow{O{Q}_{1}}$+$\overrightarrow{O{Q}_{2}}$+…+$\overrightarrow{O{Q}_{n}}$,
∴$\overrightarrow{O{P}_{1}}$$+\overrightarrow{O{P}_{2}}$$+\overrightarrow{O{P}_{3}}$+…+$\overrightarrow{O{P}_{n}}$=$\overrightarrow{O{Q}_{1}}$+$\overrightarrow{O{Q}_{2}}$+…+$\overrightarrow{O{Q}_{n}}$=$\overrightarrow{0}$;
综上所述,
$\overrightarrow{O{P}_{1}}$$+\overrightarrow{O{P}_{2}}$$+\overrightarrow{O{P}_{3}}$+…+$\overrightarrow{O{P}_{n}}$=$\overrightarrow{0}$.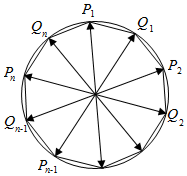
点评 本题考查了分类讨论与数形结合的思想方法应用及平面向量的应用.

 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{7}{2}$ | D. | $\frac{11}{2}$ |
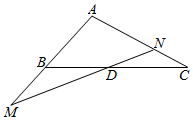 如图,在△ABC中,点D是BC上一点,且$\overrightarrow{BD}$=λ$\overrightarrow{DC}$,过点D的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AM}$,$\overrightarrow{AC}$=$\frac{3}{2}$$\overrightarrow{AN}$,则λ的值为( )
如图,在△ABC中,点D是BC上一点,且$\overrightarrow{BD}$=λ$\overrightarrow{DC}$,过点D的直线分别交直线AB、AC于不同的两点M、N,若$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{AM}$,$\overrightarrow{AC}$=$\frac{3}{2}$$\overrightarrow{AN}$,则λ的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
| A. | a>0 | B. | 0<a<1 | C. | 1<a<3 | D. | a>1 |