题目内容
已知复数z=
在复平面内对应的点z(x,y)位于( )
| i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:化简复数为a+bi的形式,即可得到复数在复平面内对应的点所在象限.
解答:
解:复数z=
=
=
=
+
i,
复数z=
(其中i为虚数单位)在复平面内对应的点(
,
).
在第一象限.
故选:A.
| i |
| 1+i |
| i(1-i) |
| (1+i)(1-i) |
| 1+i |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
复数z=
| i |
| 1+i |
| 1 |
| 2 |
| 1 |
| 2 |
在第一象限.
故选:A.
点评:本题考查复数代数形式的混合运算,复数对应的点的几何意义,基本知识的考查.

练习册系列答案
相关题目
变量 x y、满足线性约束条件
,则目标函数 z=kx-y,仅在点(0,2)取得最小值,则k的取值范围是( )
|
| A、k<-3 |
| B、k>1? |
| C、-3<k<1 |
| D、-1<k<1 |
将函数y=cos(
x+
)的图象经过怎样的平移,可以得到函数y=cos(
x)的图象( )
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
如图是一个几何体的三视图,由图中数据可知该几何体中最长棱的长度是( )


| A、6 | ||
B、2
| ||
| C、5 | ||
D、
|
已知复数z=(1-i)(1+2i),其中i为虚数单位,则
的实部为( )
. |
| z |
| A、-3 | B、1 | C、-1 | D、3 |
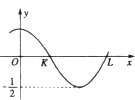 设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,KL=1,则f(
设偶函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,KL=1,则f(| 1 |
| 6 |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、
|
如图所示的程序框图,运行相应的程序,输出的S值为( )


| A、14 | B、20 | C、30 | D、55 |