题目内容
首项为正数的数列{an}满足an+1=
(
+3),若数列{an}是递增数列,则a1的取值范围是 .
| 1 |
| 4 |
| a | 2 n |
考点:数列递推式
专题:等差数列与等比数列
分析:由已知得an+1-an=
(an-1)(an-3),从而an+1>an当且仅当an<1或an>3.若0<ak<1,则0<ak+1<
=1,若ak>3,则ak+1>3.由此能求出对一切n∈N+都有an+1>an的充要条件是0<a1<1或a1>3.
| 1 |
| 4 |
| 1+3 |
| 4 |
解答:
解:∵an+1=
(
+3),
∴an+1-an=
(an-1)(an-3),
∴an+1>an当且仅当an<1或an>3.
另一方面,若0<ak<1,则0<ak+1<
=1,
若ak>3,则ak+1>
=3.
根据数学归纳法得,0<a1<1,∴0<an<1,?n∈N+.
由a1>3,得an>3,?n∈N+.
综上所述,对一切n∈N+都有an+1>an的充要条件是0<a1<1或a1>3.
∴a1的取值范围是(0,1)∪(3,+∞).
故答案为:(0,1)∪(3,+∞).
| 1 |
| 4 |
| a | 2 n |
∴an+1-an=
| 1 |
| 4 |
∴an+1>an当且仅当an<1或an>3.
另一方面,若0<ak<1,则0<ak+1<
| 1+3 |
| 4 |
若ak>3,则ak+1>
| 32+3 |
| 4 |
根据数学归纳法得,0<a1<1,∴0<an<1,?n∈N+.
由a1>3,得an>3,?n∈N+.
综上所述,对一切n∈N+都有an+1>an的充要条件是0<a1<1或a1>3.
∴a1的取值范围是(0,1)∪(3,+∞).
故答案为:(0,1)∪(3,+∞).
点评:本题考查数列的首项的取值范围的求法,是基础题,解题时要认真审题,注意数列的性质的合理运用.

练习册系列答案
相关题目
若An3=12Cn2,则n等于( )
| A、8 | B、4 | C、3或4 | D、5或6 |
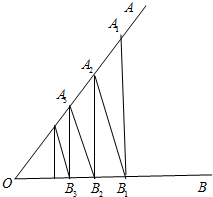 如图,相交于点O的两条直线OA,OB,在OA上取一点A,作A1B1⊥OB,作B1A2⊥OA,作A2B2⊥OB…一直无限地作下去,若已知A1B1=7,B1A2=6,则所有垂线长度的和等于
如图,相交于点O的两条直线OA,OB,在OA上取一点A,作A1B1⊥OB,作B1A2⊥OA,作A2B2⊥OB…一直无限地作下去,若已知A1B1=7,B1A2=6,则所有垂线长度的和等于