题目内容
19．
将正方体切去一个三棱锥得到几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{22}{3}$ | B． | $\frac{20}{3}$ | C． | $\frac{16}{3}$ | D． | 6 |
分析 由已知中的三视图可得：该几何体是一个正方体切去一个三棱锥所得的组合体，进而得到答案．
解答 解：由已知中的三视图可得：该几何体是一个正方体切去一个三棱锥所得的组合体，
正方体的体积为：8，
三棱锥的体积为：$\frac{1}{3}$×$\frac{1}{2}$×2×2×1=$\frac{2}{3}$，
故组合体的体积V=8-$\frac{2}{3}$=$\frac{22}{3}$，
故选：A．
点评 本题考查的知识点是棱锥的体积与表面积，棱柱的体积与表面积，简单几何体的三视图，难度中档．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
10．在等差数列{an}中，a2=2，a6=10，则a10=（ ）
| A． | 18 | B． | 16 | C． | 14 | D． | 12 |
7．要得到函数$y=cos（\frac{x}{2}-\frac{π}{3}）$的图象，只需将函数$y=cos\frac{x}{2}$的图象（ ）
| A． | 向左平移$\frac{π}{3}$个单位 | B． | 向右平移$\frac{π}{3}$个单位 | ||
| C． | 向左平移$\frac{2π}{3}$个单位 | D． | 向右平移$\frac{2π}{3}$个单位 |
14．下列函数求导错误的是（ ）
| A． | （$\sqrt{x}$）′=$\frac{1}{2\sqrt{x}}$ | B． | （$\frac{1}{x}$）′=-$\frac{1}{{x}^{2}}$ | C． | （lnx）′=$\frac{1}{x}$ | D． | （e-x）′=e-x |
4．一个几何体的三视图如图所示，该几何体的体积为（ ）
| A． | 24-π | B． | 24-3π | C． | $8-\frac{4π}{3}$ | D． | $8-\frac{8π}{3}$ |
8．函数y=cosx图象上任意一点处的切线倾斜角为α，则α取值范围为（ ）
| A． | （0，π） | B． | [0，$\frac{π}{4}$] | C． | [0，$\frac{π}{4}$]∪[$\frac{3π}{4}$，π） | D． | [0，$\frac{π}{4}$]∪（$\frac{π}{2}$，$\frac{3π}{4}$] |
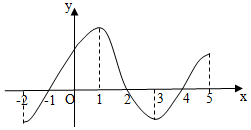如图是函数y=f（x）的导数的图象，则正确的判断是（2）（4）．