题目内容
已知函数f(x)是定义在区间[-2,2]上的偶函数,当0≤x≤2时,f(x)=x2-2x+1,若在区间[-2,2]内,函数g(x)=f(x)-kx-2k有4个零点,则实数k的取值范围是 .
考点:函数零点的判定定理
专题:计算题,作图题,函数的性质及应用
分析:首先由定义化简函数,作出函数的图象,问题化为过点A(-2,0)的直线与函数f(x)有4个不同的交点,由图象解出.
解答:
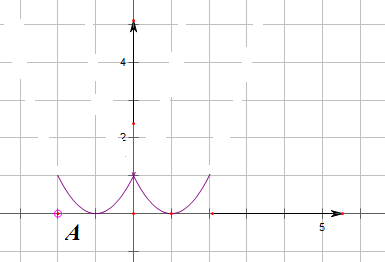 解:∵函数f(x)是定义在区间[-2,2]上的偶函数,当0≤x≤2时,f(x)=x2-2x+1,
解:∵函数f(x)是定义在区间[-2,2]上的偶函数,当0≤x≤2时,f(x)=x2-2x+1,
∴f(x)=
,
其图象如右图:
在区间[-2,2]内,函数g(x)=f(x)-kx-2k有4个零点,
可化为函数f(x)与直线y=kx+2k有4个不同的交点,
即过点A(-2,0)的直线与函数f(x)有4个不同的交点,
则k>0,
当有三个交点时,k=
,
故实数k的取值范围是(0,
).
 解:∵函数f(x)是定义在区间[-2,2]上的偶函数,当0≤x≤2时,f(x)=x2-2x+1,
解:∵函数f(x)是定义在区间[-2,2]上的偶函数,当0≤x≤2时,f(x)=x2-2x+1,∴f(x)=
|
其图象如右图:
在区间[-2,2]内,函数g(x)=f(x)-kx-2k有4个零点,
可化为函数f(x)与直线y=kx+2k有4个不同的交点,
即过点A(-2,0)的直线与函数f(x)有4个不同的交点,
则k>0,
当有三个交点时,k=
| 1 |
| 4 |
故实数k的取值范围是(0,
| 1 |
| 4 |
点评:本题考查了函数解析式的求法,学生的作图能力及转化能力,属于中档题.

练习册系列答案
相关题目
某部队练习发射炮弹,炮弹的高度h与时间t的函数关系式是h(t)=-4.9t2+14.7t+18,则炮弹在发射几秒后最高呢?( )
| A、1.3秒 | B、1.4秒 |
| C、1.5秒 | D、1.6秒 |
设全集U={1,2,3,4,5},若P∩Q={2},(∁UP)∩Q={4},(∁UP)∩(∁UQ)={1,5},则下列结论正确的是( )
| A、3∉P 且3∉Q |
| B、3∈P 且3∉Q |
| C、3∉P 且3∈Q |
| D、3∈P且3∈Q |