若数列{an}的前n项和Sn=$\frac{2}{3}$an-$\frac{2}{3}$.则数列{an}的通项公式an=(-2)n．题目和参考答案——青夏教育精英家教网—

题目内容

5．若数列{a_n}的前n项和S_n=$\frac{2}{3}$a_n-$\frac{2}{3}$，则数列{a_n}的通项公式a_n=（-2）ⁿ．

分析利用递推关系可得：a_n=-2a_n-1，再利用等比数列的通项公式即可得出．

解答解：∵S_n=$\frac{2}{3}$a_n-$\frac{2}{3}$，
∴当n=1时，${a}_{1}=\frac{2}{3}{a}_{1}$-$\frac{2}{3}$，解得a₁=-2．
当n≥2时，a_n=S_n-S_n-1=$\frac{2}{3}$a_n-$\frac{2}{3}$-$（\frac{2}{3}{a}_{n-1}-\frac{2}{3}）$，化为：a_n=-2a_n-1．
∴数列{a_n}是等比数列，首项与公比都为-2．
∴a_n=（-2）ⁿ．
故答案为：（-2）ⁿ．

点评本题考查了递推关系、等比数列的通项公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案

相关题目

4．等比数列{a_n}的前n项和为S_n，若公比q=4，S₃=21，则（　　）

16．

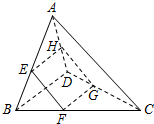如图，在四面体A-BCD中，AC与BD互相垂直，且长度分别为2和3，平行于这两条棱的平面与边AB、BC、CD、DA分别相交于点E、F、G、H，记四边形EFGH的面积为y，设$\frac{BE}{AB}$=x，则（　　）

	A．	函数f（x）的值域为（0，1]		B．	函数y=f（x）满足f（x）=f（2-x）
	C．	函数y=f（x）的最大值为2		D．	函数y=f（x）在（0，$\frac{1}{2}$）上单调递增

13．

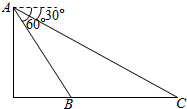如图，从高为$200\sqrt{3}$米的气球（A）上测量铁桥（BC）的长，如果测得桥头B的俯角是60°，桥头C的俯角是30°，则桥BC长为400米．