题目内容
设f（x）=-x3+x2+tx+t 在（-2，2）上是增函数，求t的取值范围为 ．
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：求函数的导数，利用函数的单调性和导数之间的关系，转化为f′（x）≥0在（-2，2）恒成立，利用二次函数的图象和性质，即可得到结论．
解答：
解：∵f（x）=-x3+x2+tx+t，
∴f′（x）=-3x2+2x+t，
要使函数f（x）=-x3+x2+tx+t 在（-2，2）上是增函数，
则f′（x）=-3x2+2x+t≥0在（-2，2）恒成立，
即t≥3x2-2x在（-2，2）上恒成立，
设g（x）=3x2-2x，则g（x）=3x2-2x=3（x-
）2-
，
∵x∈（-2，2），
∴-
≤g（x）＜16，
∴t≥16，
故答案为：[16，+∞）
∴f′（x）=-3x2+2x+t，
要使函数f（x）=-x3+x2+tx+t 在（-2，2）上是增函数，
则f′（x）=-3x2+2x+t≥0在（-2，2）恒成立，
即t≥3x2-2x在（-2，2）上恒成立，
设g（x）=3x2-2x，则g（x）=3x2-2x=3（x-
| 1 |
| 3 |
| 1 |
| 3 |
∵x∈（-2，2），
∴-
| 1 |
| 3 |
∴t≥16，
故答案为：[16，+∞）
点评：本题主要考查函数单调性和导数之间的关系，利用函数恒成立是解决本题的关键．
练习册系列答案
相关题目
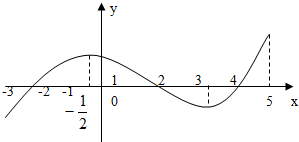如果函数y=f（x）的导函数的图象如图所示，给出下列判断：