题目内容
已知函数f(x)=a-
.
(Ⅰ)求证:不论a为何实数f(x)总是为增函数;
(Ⅱ)确定a的值,使f(x)为奇函数,并说明理由;
(Ⅲ)当f(x)为奇函数时,若
<4x+a恒成立,求实数a的取值范围.
| 1 |
| 2x+1 |
(Ⅰ)求证:不论a为何实数f(x)总是为增函数;
(Ⅱ)确定a的值,使f(x)为奇函数,并说明理由;
(Ⅲ)当f(x)为奇函数时,若
| 1 | ||
|
考点:函数恒成立问题,函数奇偶性的性质
专题:函数的性质及应用,不等式的解法及应用
分析:(Ⅰ)直接利用函数单调性的定义加以证明;
(Ⅱ)由函数是定义域为R上的奇函数,借助于f(0)=0求得a的值,然后利用奇函数的定义验证;
(Ⅲ)由函数是奇函数得到f(x)的解析式,代入
<4x+a后分离参数a,然后利用换元法及配方法求出函数的最值,则答案可求.
(Ⅱ)由函数是定义域为R上的奇函数,借助于f(0)=0求得a的值,然后利用奇函数的定义验证;
(Ⅲ)由函数是奇函数得到f(x)的解析式,代入
| 1 | ||
|
解答:
(Ⅰ)证明:函数f(x)=a-
的定义域为R,
任设x1,x2∈(-∞,+∞),且x1<x2,
则f(x1)-f(x2)=a-
-a+
=
.
∵x1<x2,
∴2x1-2x20,
∴f(x1)<f(x2).
即不论a为何实数f(x)总是为增函数;
(Ⅱ)解:∵f(x)为定义在实数集上的奇函数,
∴对于任意实数x都有f(-x)=-f(x),
令x=0,则f(0)=f(-0)=-f(0),f(0)=0.
∴a-
=0,即a=
.
则f(x)=
-
.
∵f(x)+f(-x)=
-
+
-
=1-
=0.
∴f(-x)=-f(x).
即当a=
时,函数f(x)为奇函数;
(Ⅲ)解:当f(x)为奇函数时,f(x)=
-
,
由
<4x+a,得2x+1<4x+a.
即a>-4x+2x+1恒成立.
令t=2x,则t>0,
-4x+2x+1=-t2+t+1=-(t-
)2+
≤
.
当且仅当t=
时取等号.
∴a>
.
| 1 |
| 2x+1 |
任设x1,x2∈(-∞,+∞),且x1<x2,
则f(x1)-f(x2)=a-
| 1 |
| 2x1+1 |
| 1 |
| 2x2+1 |
| 2x1-2x2 |
| (2x1+1)(2x2+1) |
∵x1<x2,
∴2x1-2x20,
∴f(x1)<f(x2).
即不论a为何实数f(x)总是为增函数;
(Ⅱ)解:∵f(x)为定义在实数集上的奇函数,
∴对于任意实数x都有f(-x)=-f(x),
令x=0,则f(0)=f(-0)=-f(0),f(0)=0.
∴a-
| 1 |
| 2 |
| 1 |
| 2 |
则f(x)=
| 1 |
| 2 |
| 1 |
| 2x+1 |
∵f(x)+f(-x)=
| 1 |
| 2 |
| 1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2-x+1 |
| 2x+2-x+2 |
| 2x+2-x+2 |
∴f(-x)=-f(x).
即当a=
| 1 |
| 2 |
(Ⅲ)解:当f(x)为奇函数时,f(x)=
| 1 |
| 2 |
| 1 |
| 2x+1 |
由
| 1 | ||
|
即a>-4x+2x+1恒成立.
令t=2x,则t>0,
-4x+2x+1=-t2+t+1=-(t-
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
当且仅当t=
| 1 |
| 2 |
∴a>
| 5 |
| 4 |
点评:本题考查了函数的性质,考查了函数的单调性和奇偶性的证明方法,训练了利用分离参数法求变量的取值范围,考查了配方法,是压轴题.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
在复平面内,复数
(i是复数单位)对应的点在第几象限( )
| 1 | ||
-
|
| A、一 | B、二 | C、三 | D、四 |
对任意实数a,下列等式正确的是( )
A、(a
| ||||||
B、(a
| ||||||
C、(a -
| ||||||
D、(a
|
现有四个函数:①y=x•sinx;②y=x•cosx;③y=x•|cosx|;④y=x•2x的图象(部分)如下:
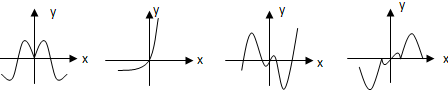
则按照从左到右图象对应的函数序号安排正确的一组是( )

则按照从左到右图象对应的函数序号安排正确的一组是( )
| A、①④③② | B、③④②① |
| C、④①②③ | D、①④②③ |

 在抛物线y2=16x内有一点G(4,4)抛物线的焦点为F,若以F,G为焦点作一个与抛物线相交且长轴最短的椭圆,则此椭圆的离心率为
在抛物线y2=16x内有一点G(4,4)抛物线的焦点为F,若以F,G为焦点作一个与抛物线相交且长轴最短的椭圆,则此椭圆的离心率为