题目内容
已知函数f(x)与函数g(x)=log
x的图象关于直线y=x对称,则f(-2)= .
| 1 |
| 2 |
考点:反函数
专题:函数的性质及应用
分析:由函数f(x)与函数g(x)=log
x的图象关于直线y=x对称,可得函数f(x)与函数g(x)=log
x互为反函数,即f(x)=(
)x,代入x=-2,可得答案.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵函数f(x)与函数g(x)=log
x的图象关于直线y=x对称,
∴函数f(x)与函数g(x)=log
x互为反函数,
∴f(x)=(
)x,
∴f(-2)=4,
故答案为:4.
| 1 |
| 2 |
∴函数f(x)与函数g(x)=log
| 1 |
| 2 |
∴f(x)=(
| 1 |
| 2 |
∴f(-2)=4,
故答案为:4.
点评:本题考查的知识点是反函数,其中根据函数f(x)与函数g(x)=log
x的图象关于直线y=x对称,得到函数f(x)与函数g(x)=log
x互为反函数,是解答的关键.
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
函数f(x)=ax2+bx+5满足条件f(-1)=f(3),则f(2)的值为( )
| A、5 | B、6 |
| C、8 | D、与a,b的值有关 |
设a=log
3,b=(
)0.2,c=2
,则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、a<b<c |
| B、b<a<c |
| C、b<c<a |
| D、a<c<b |
不等式x2≥5x的解集是( )
| A、[0,5] |
| B、(-∞,0]∪[5,+∞) |
| C、(-∞,0] |
| D、[5,+∞) |
 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0|)的图象如下图所示,则f(1)+f(2)+f(3)+…+f(2014)=
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0|)的图象如下图所示,则f(1)+f(2)+f(3)+…+f(2014)=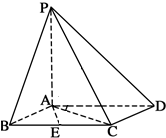 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.