题目内容
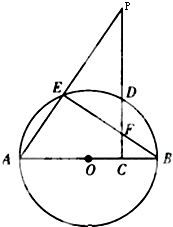 如图,AB为圆O的直径,P为圆O外一点,过P点作PC⊥AB于C,交圆O于D点,PA交圆O于E点,BE交PC于F点.
如图,AB为圆O的直径,P为圆O外一点,过P点作PC⊥AB于C,交圆O于D点,PA交圆O于E点,BE交PC于F点.(Ⅰ)求证:∠P=∠ABE;
(Ⅱ)求证:CD2=CF•CP.
考点:与圆有关的比例线段
专题:选作题,立体几何
分析:(Ⅰ)在Rt△ACP中,∠P=90°-∠PAB;在Rt△ABE中,∠ABE=90°-∠PAB,即可证明:∠P=∠ABE;
(Ⅱ)证明△BCF∽△PCA,即可证明CD2=CF•CP.
(Ⅱ)证明△BCF∽△PCA,即可证明CD2=CF•CP.
解答:
证明:(Ⅰ)∠AEB=∠ACP=90°,∴在Rt△ACP中,∠P=90°-∠PAB;
在Rt△ABE中,∠ABE=90°-∠PAB,∴∠P=∠ABE.….(5分)
(Ⅱ)在Rt△ADB中,CD2=AC•CB,由①得△BCF∽△PCA,∴
=
,
∴CD2=BC•AC=CF•CP,∴CD2=CF•CP.….10分
在Rt△ABE中,∠ABE=90°-∠PAB,∴∠P=∠ABE.….(5分)
(Ⅱ)在Rt△ADB中,CD2=AC•CB,由①得△BCF∽△PCA,∴
| BC |
| PC |
| CF |
| AC |
∴CD2=BC•AC=CF•CP,∴CD2=CF•CP.….10分
点评:本题考查与圆有关的比例线段,考查三角形相似的判定,属于中档题.

练习册系列答案
相关题目
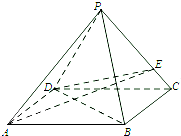 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,平面PBD⊥平面ABCD,AD=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,平面PBD⊥平面ABCD,AD=2,PD=2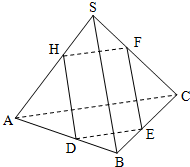 如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,SA=SB=SC=4,平面DEFH分别与三棱锥S-ABC的四条棱AB、BC、SC、SA交于D、E、F、H,若直线SB∥平面DEFH,直线AC∥平面DEFH,则平面DEFH与平面SAC所成的二面角(锐角)的余弦值等于
如图,在三棱锥S-ABC中,△ABC是边长为2的正三角形,SA=SB=SC=4,平面DEFH分别与三棱锥S-ABC的四条棱AB、BC、SC、SA交于D、E、F、H,若直线SB∥平面DEFH,直线AC∥平面DEFH,则平面DEFH与平面SAC所成的二面角(锐角)的余弦值等于