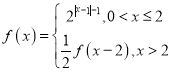题目内容
【题目】已知椭圆
的左、右焦点为
、
，
，若圆Q方程
，且圆心Q在椭圆上．
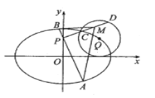
（1）求椭圆
的方程；
（2）已知直线
交椭圆于A、B两点，过直线
上一动点P作与垂直的直线
交圆Q于C、D两点，M为弦CD中点，
的面积是否为定值？若为定值，求出此定值；若不为定值，说明你的理由．
【答案】（1）
（2）为定值，定值是
【解析】
（1）由椭圆的定义求得
，再根据焦点坐标得
，再由
得到
的值，从而得到椭圆的方程；
（2）设
，
，将直线
的方程代入椭圆方程，利用弦长公式求得
；由题设条件得
，从而有
，所以
的面积为定值，利用面积公式可得答案.
解：（1）由题意可知：
，
，
，
∴
，
，
∴椭圆
的方程为.
（2）设，，由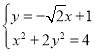
消去y，得
，
∴
,
∵M为线段CD中点，∴
，
又∵
，，∴，
又点Q到的距离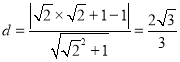
，
∴
.
练习册系列答案
春雨教育同步作文系列答案
相关题目
