题目内容
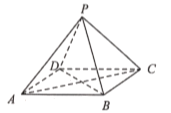
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)通过菱形的性质证得![]() ,通过等腰三角形的性质证得
,通过等腰三角形的性质证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,从而证得平面
,从而证得平面![]() 平面
平面![]() .
.
(2)方法一通过几何法作出二面角![]() 的平面角,解三角形求得二面角的余弦值.方法而通过建立空间直角坐标系,利用平面
的平面角,解三角形求得二面角的余弦值.方法而通过建立空间直角坐标系,利用平面![]() 和平面
和平面![]() 的法向量,计算出二面角的余弦值.
的法向量,计算出二面角的余弦值.
(1)证明:记![]() ,连接
,连接![]() .
.
因为底面![]() 是菱形,
是菱形,
所以![]() ,
,![]() 是
是![]() 的中点.
的中点.
因为![]() ,所以
,所以![]() .
.
因为![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)因为底面![]() 是菱形,
是菱形,![]() ,
,![]() ,
,
所以![]() 是等边三角形,即
是等边三角形,即![]() .
.
因为![]() ,所以
,所以![]() .
.
又![]() ,
,![]() ,所以
,所以![]() ,
,
即![]() .
.
方法一:因为![]() 是
是![]() 的中点,所以
的中点,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() 和
和![]() 都是等腰三角形.
都是等腰三角形.
取![]() 中点
中点![]() ,连接
,连接![]() ,则
,则![]() ,且
,且![]() ,
,
所以![]() 是二面角
是二面角![]() 的平面角.
的平面角.
因为![]() ,且
,且![]() ,
,
所以![]() .
.
因为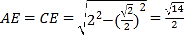 ,
,
![]() ,
,
所以![]() .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.
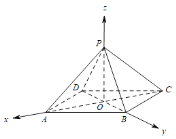
方法二:如图,以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]()
由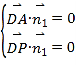 ,得
,得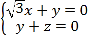 ,
,
令![]() ,得
,得![]() .
.
同理,可求平面![]() 的法向量
的法向量![]() .
.
所以

![]() .
.
所以,二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】汽车尾气中含有一氧化碳(![]() ),碳氢化合物(
),碳氢化合物(![]() )等污染物,是环境污染的主要因素之一,汽车在使用若干年之后排放的尾气中的污染物会出现递增的现象,所以国家根据机动车使用和安全技术、排放检验状况,对达到报废标准的机动车实施强制报废.某环保组织为了解公众对机动车强制报废标准的了解情况,随机调查了100人,所得数据制成如下列联表:
)等污染物,是环境污染的主要因素之一,汽车在使用若干年之后排放的尾气中的污染物会出现递增的现象,所以国家根据机动车使用和安全技术、排放检验状况,对达到报废标准的机动车实施强制报废.某环保组织为了解公众对机动车强制报废标准的了解情况,随机调查了100人,所得数据制成如下列联表:
不了解 | 了解 | 总计 | |
女性 |
|
| 50 |
男性 | 15 | 35 | 50 |
总计 |
|
| 100 |
(1)若从这100人中任选1人,选到了解机动车强制报废标准的人的概率为![]() ,问是否有
,问是否有![]() 的把握认为“对机动车强制报废标准是否了解与性别有关”?
的把握认为“对机动车强制报废标准是否了解与性别有关”?
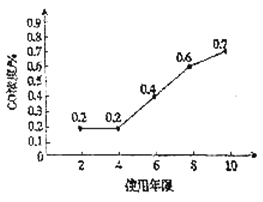
(2)该环保组织从相关部门获得某型号汽车的使用年限与排放的尾气中![]() 浓度的数据,并制成如图所示的折线图,若该型号汽车的使用年限不超过15年,可近似认为排放的尾气中
浓度的数据,并制成如图所示的折线图,若该型号汽车的使用年限不超过15年,可近似认为排放的尾气中![]() 浓度
浓度![]() 与使用年限
与使用年限![]() 线性相关,试确定
线性相关,试确定![]() 关于
关于![]() 的回归方程,并预测该型号的汽车使用12年排放尾气中的
的回归方程,并预测该型号的汽车使用12年排放尾气中的![]() 浓度是使用4年的多少倍.
浓度是使用4年的多少倍.
附: (
(![]() )
)
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:用最小二乘法求线性回归方程系数公式: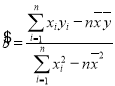 ,
,![]() .
.