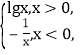题目内容
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,上顶点为
,上顶点为![]() .已知椭圆的短轴长为4,离心率为
.已知椭圆的短轴长为4,离心率为![]() .
.
(Ⅰ)求椭圆的方程;
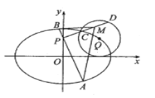
(Ⅱ)设点![]() 在椭圆上,且异于椭圆的上、下顶点,点
在椭圆上,且异于椭圆的上、下顶点,点![]() 为直线
为直线![]() 与
与![]() 轴的交点,点
轴的交点,点![]() 在
在![]() 轴的负半轴上.若
轴的负半轴上.若![]() (
(![]() 为原点),且
为原点),且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() 或
或![]() .
.
【解析】
(Ⅰ)由题意得到关于a,b,c的方程,解方程可得椭圆方程;
(Ⅱ)联立直线方程与椭圆方程确定点P的坐标,从而可得OP的斜率,然后利用斜率公式可得MN的斜率表达式,最后利用直线垂直的充分必要条件得到关于斜率的方程,解方程可得直线的斜率.
(Ⅰ) 设椭圆的半焦距为![]() ,依题意,
,依题意,![]() ,又
,又![]() ,可得
,可得![]() ,b=2,c=1.
,b=2,c=1.
所以,椭圆方程为![]() .
.
(Ⅱ)由题意,设![]() .设直线
.设直线![]() 的斜率为
的斜率为![]() ,
,
又![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,与椭圆方程联立
,与椭圆方程联立 ,
,
整理得![]() ,可得
,可得![]() ,
,
代入![]() 得
得![]() ,
,
进而直线![]() 的斜率
的斜率![]() ,
,
在![]() 中,令
中,令![]() ,得
,得![]() .
.
由题意得![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() .
.
由![]() ,得
,得![]() ,
,
化简得![]() ,从而
,从而![]() .
.
所以,直线![]() 的斜率为
的斜率为![]() 或
或![]() .
.

练习册系列答案
相关题目