题目内容
【题目】己知函数![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,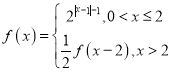 ,则函数
,则函数![]() 在
在![]() 上的所有零点之和为( )
上的所有零点之和为( )
A.7B.8C.9D.10
【答案】B
【解析】
由已知可分析出函数![]() 是偶函数,则其零点必然关于原点对称,故
是偶函数,则其零点必然关于原点对称,故![]() 在
在![]() 上所有的零点的和为
上所有的零点的和为![]() ,则函数
,则函数![]() 在
在![]() 上所有的零点的和,即函数
上所有的零点的和,即函数![]() 在
在![]() 上所有的零点之和,求出
上所有的零点之和,求出![]() 上所有零点,可得答案.
上所有零点,可得答案.
解:![]() 函数
函数![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数,![]() .
.
又![]() 函数
函数![]() ,
,
![]() ,
,
![]() 函数
函数![]() 是偶函数,
是偶函数,
![]() 函数
函数![]() 的零点都是以相反数的形式成对出现的.
的零点都是以相反数的形式成对出现的.
![]() 函数
函数![]() 在
在![]() 上所有的零点的和为
上所有的零点的和为![]() ,
,
![]() 函数
函数![]() 在
在![]() 上所有的零点的和,即函数
上所有的零点的和,即函数![]() 在
在![]() 上所有的零点之和.
上所有的零点之和.
由![]() 时,
时,![]() ,
,
即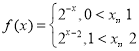
![]() 函数
函数![]() 在
在![]() 上的值域为
上的值域为![]() ,当且仅当
,当且仅当![]() 时,
时,![]()
又![]() 当
当![]() 时,
时,![]()
![]() 函数
函数![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
函数![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
函数![]() 在
在![]() 上的值域为
上的值域为![]() ,当且仅当
,当且仅当![]() 时,
时,![]() ,
,
函数![]() 在
在![]() 上的值域为
上的值域为![]() ,当且仅当
,当且仅当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 上恒成立,
上恒成立,![]() 在
在![]() 上无零点,
上无零点,
同理![]() 在
在![]() 上无零点,
上无零点,
依此类推,函数![]() 在
在![]() 无零点,
无零点,
综上函数![]() 在
在![]() 上的所有零点之和为8
上的所有零点之和为8
故选:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目