题目内容
5.设$\overrightarrow{a}$=(cos25°sin25°)$\overrightarrow{b}$=(sin20°,cos20°),若t是实数,且$\overrightarrow{μ}$=$\overrightarrow{a}$+t$\overrightarrow{b}$,求|$\overrightarrow{μ}$|的最小值.分析 由平面向量的坐标运算求出$\overrightarrow{μ}$=$\overrightarrow{a}$+t$\overrightarrow{b}$的坐标,求模后利用二次函数求最值.
解答 解:∵$\overrightarrow{a}$=(cos25°,sin25°)$\overrightarrow{b}$=(sin20°,cos20°),
∴$\overrightarrow{μ}$=$\overrightarrow{a}$+t$\overrightarrow{b}$=(cos25°,sin25°)+t(sin20°,cos20°)=(cos25°+tsin20°,sin25°+tcos20°),
则|$\overrightarrow{μ}$|=$\sqrt{(cos25°+tsin20°)^{2}+(sin25°+tcos20°)^{2}}$
=$\sqrt{1+{t}^{2}+2t•sin45°}$=$\sqrt{{t}^{2}+\sqrt{2}t+1}$,
∴当t=$-\frac{\sqrt{2}}{2}$时,|$\overrightarrow{μ}$|有最小值为$\sqrt{(-\frac{\sqrt{2}}{2})^{2}+\sqrt{2}×(-\frac{\sqrt{2}}{2})+1}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查平面向量的坐标运算,考查了向量模的求法,是基础题.

练习册系列答案
相关题目
14.tan23°+tan97°-$\sqrt{3}$tan23°tan97°=( )
| A. | -2 | B. | -2$\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 0 |

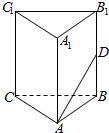 如图所示,在正三棱柱ABC-A1B1C1中,已知AB=1,D是棱BB1上的点,且BD=1,求:
如图所示,在正三棱柱ABC-A1B1C1中,已知AB=1,D是棱BB1上的点,且BD=1,求: