题目内容
13.若函数f(x)=x3,f′(a)=3,求a的值.分析 利用导数的运算性质即可得出.
解答 解:函数f(x)=x3,∴f′(x)=3x2.
∵f′(a)=3,
∴3a2=3,
解得a=±1.
点评 本题考查了导数的运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知函数f(x)=sinx+cosx.
(1)求函数F(x)=f(x)f(-x)+f2(x)的单调递增区间;
(2)设△ABC的三边a,b,c满足b2=ac,且边b所对的角为B,求函数f(B)的值域.
(1)求函数F(x)=f(x)f(-x)+f2(x)的单调递增区间;
(2)设△ABC的三边a,b,c满足b2=ac,且边b所对的角为B,求函数f(B)的值域.
8.已知a>0,b>0且ab-(a+b)≥1,则( )
| A. | a+b≥2($\sqrt{2}$+1) | B. | a+b≤$\sqrt{2}$+1 | C. | a+b≤($\sqrt{2}$+1)2 | D. | a+b>2($\sqrt{2}$+1) |
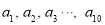 的平均数为
的平均数为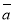 ,样本
,样本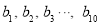 的平均数为
的平均数为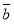 ,那么样本
,那么样本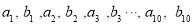 的平均数为( )
的平均数为( )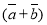 B.
B.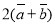 C.
C. 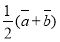 D.
D.