题目内容
14.tan23°+tan97°-$\sqrt{3}$tan23°tan97°=( )| A. | -2 | B. | -2$\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 0 |
分析 由tan120°=tan(23°+97°),展开两角和的正切后整理得答案.
解答 解:∵tan120°=tan(23°+97°)=$\frac{tan23°+tan97°}{1-tan23°tan97°}$,
且$tan120°=-\sqrt{3}$,
∴$\frac{tan23°+tan97°}{1-tan23°tan97°}$=-$\sqrt{3}$,
则$tan23°+tan97°=-\sqrt{3}+\sqrt{3}tan23°tan97°$,
即tan23°+tan97°-$\sqrt{3}$tan23°tan97°=$-\sqrt{3}$.
故选:C.
点评 本题考查两角和与差的正切,考查灵活变形能力,是基础题.

练习册系列答案
相关题目
10.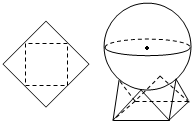 用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )
用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )
 用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )
用一个边长为2的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,现将半径为$\sqrt{2}$的球体放置于蛋巢上,则球体球心与蛋巢底面的距离为( )| A. | $\frac{\sqrt{2}+2}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | C. | $\frac{\sqrt{10}+\sqrt{2}}{2}$ | D. | $\frac{\sqrt{10}-\sqrt{2}}{2}$ |

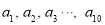 的平均数为
的平均数为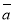 ,样本
,样本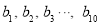 的平均数为
的平均数为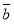 ,那么样本
,那么样本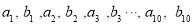 的平均数为( )
的平均数为( )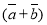 B.
B.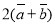 C.
C. 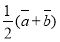 D.
D.