题目内容
15.已知直线l1:x-3y-2=0与直线l2:2x+y-4=0相交于点C,(1)求以C为圆心,半径为1的圆C的方程;
(2)在(1)的条件下,过点M(1.3)的直线1与圆C相切,求直线1的方程.
分析 (1)由直线l1:x-3y-2=0与直线l2:2x+y-4=0联立,可得C的坐标,即可求以C为圆心,半径为1的圆C的方程;
(2)分类讨论,利用过点M(1.3)的直线1与圆C相切,圆心到直线的距离d=r,即可求直线1的方程.
解答 解:(1)由直线l1:x-3y-2=0与直线l2:2x+y-4=0联立,可得x=2,y=0,
∴C(2,0),
∴以C为圆心,半径为1的圆C的方程为(x-2)2+y2=1;
(2)斜率不存在时,x=1,满足题意;
斜率存在时,设直线1的方程为y-3=k(x-1),即kx-y-k+3=0,
∴圆心到直线的距离d=$\frac{|k+3|}{\sqrt{{k}^{2}+1}}$=1,
∴k=-$\frac{4}{3}$,
∴直线1的方程为4x+3y-13=0.
点评 本题考查直线、圆的方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.曲线y=ex和曲线y=lnx分别与直线x=x0交于点A,B,且曲线y=ex在点A处的切线与曲线y=lnx在点B处的切线平行,则x0在下列哪个区间内( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
20.抛物线y=x2的一组斜率为2的平行弦中点的轨迹是( )
| A. | 圆 | B. | 椭圆 | C. | 抛物线 | D. | 射线(不含端点) |
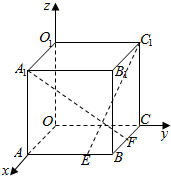 如图,在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是棱AB、BC上的动点,且AE=BF=x,其中0≤x≤a,以O为原点建立空间直角坐标系O-xyz.
如图,在棱长为a的正方体OABC-O1A1B1C1中,E,F分别是棱AB、BC上的动点,且AE=BF=x,其中0≤x≤a,以O为原点建立空间直角坐标系O-xyz.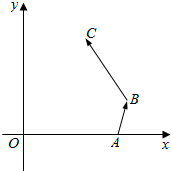 如图,在平面直角坐标系中,|$\overrightarrow{OA}$|=2|$\overrightarrow{AB}$|=2,∠OAB=$\frac{2π}{3}$,$\overrightarrow{BC}$=(-1,$\sqrt{3}$).
如图,在平面直角坐标系中,|$\overrightarrow{OA}$|=2|$\overrightarrow{AB}$|=2,∠OAB=$\frac{2π}{3}$,$\overrightarrow{BC}$=(-1,$\sqrt{3}$).