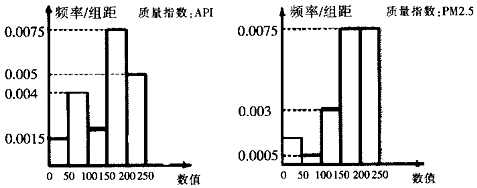
题目内容
17.若${({{x^2}+\frac{a}{x}})^n}$的展开式中,二项式系数和为64,所有项的系数和为729,则a的值为-4或2.分析 根据二项式系数和为2n求出n的值,再x=1得展开式中所有项的系数和,即可求出a的值.
解答 解:${({{x^2}+\frac{a}{x}})^n}$展开式中,二项式系数和为64,
∴2n=64,
解得n=6;
令x=1,得展开式中所有项的系数和为
(1+a)6=729,
∴1+a=±3,
解得a=-4或2.
故答案为:-4或2.
点评 本题考查了二项式定理的应用问题,是基础题.

练习册系列答案
相关题目
7.函数f(x)=sin(ωx+φ)(x∈R,ω>0,-π≤φ<π)的部分图象如图所示,则( )
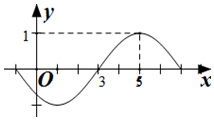

| A. | ω=$\frac{π}{2}$,φ=-π | B. | ω=$\frac{π}{2}$,φ=0 | C. | ω=$\frac{π}{4}$,φ=$\frac{π}{4}$ | D. | ω=$\frac{π}{4}$,φ=-$\frac{3π}{4}$ |
12.已知函数:①y=x3+3x2;②$y=\frac{{{e^x}+{e^{-x}}}}{2}$;③$y={log_2}\frac{3-x}{3+x}$;④y=xsinx,从中任取两个函数,则这两函数奇偶性相同的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
9.过点P(1,2)的直线与圆x2+y2=1相切,且与直线ax+y-1=0垂直,则实数a的值为( )
| A. | 0 | B. | $-\frac{4}{3}$ | C. | 0或$\frac{4}{3}$ | D. | $\frac{4}{3}$ |
6.设0<a<1,e为自然对数的底数,则a,ae,ea-1的大小关系为( )
| A. | ea-1<a<ae | B. | ae<a<ea-1 | C. | ae<ea-1<a | D. | a<ea-1<ae |