题目内容
6．设0＜a＜1，e为自然对数的底数，则a，ae，ea-1的大小关系为（ ）| A． | ea-1＜a＜ae | B． | ae＜a＜ea-1 | C． | ae＜ea-1＜a | D． | a＜ea-1＜ae |
分析 令f（x）=ex-1-x，（x∈（0，1））．利用导数研究函数的单调性可得ea-1与a的大小关系，再利用指数函数的单调性可得a与ae的大小关系．
解答 解：∵0＜a＜1，ae＜a，
令f（x）=ex-1-x，（x∈（0，1））．
f′（x）=ex-1＞0，
∴函数f（x）在x∈（0，1））单调递增，∴f（x）＞f（0）=1-1-0=0．
∴ea-1＞a．
∴ea-1＞a＞ae．
故选：B．
点评 本题考查了利用导数研究函数的单调性、指数函数的单调性，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
16．已知f（x）是定义在R上的可导函数，且满足（x+2）f（x）+xf'（x）＞0，则（ ）
| A． | f（x）＞0 | B． | f（x）＜0 | C． | f（x）为减函数 | D． | f（x）为增函数 |
1．已知cos（$\frac{2π}{3}$-α）=$\frac{3}{4}$，则sin（α-$\frac{π}{6}$）cos（$\frac{π}{3}$-2α）=（ ）
| A． | $\frac{3}{32}$ | B． | -$\frac{3}{32}$ | C． | $\frac{3}{16}$ | D． | -$\frac{3}{16}$ |
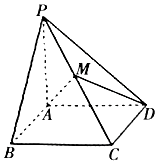如图所示，已知四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，PA=BC=1，AB=2，M为PC的中点．