题目内容
7.已知曲线f(x)=ax+cos2x在点($\frac{π}{4}$,f($\frac{π}{4}$))处的切线的斜率为-1,则实数a的值为( )| A. | 0 | B. | -1 | C. | 1 | D. | -3 |
分析 求出函数的导数,运用导数的几何意义,可得在点($\frac{π}{4}$,f($\frac{π}{4}$))处的切线的斜率,解方程即可得到所求a的值.
解答 解:f(x)=ax+cos2x的导数为f′(x)=a-2sin2x,
可得在点($\frac{π}{4}$,f($\frac{π}{4}$))处的切线的斜率为k=a-2sin$\frac{π}{2}$=a-2=-1,
解得a=1,
故选:C.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义,正确求导是解题的关键,考查运算能力,属于基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
19.已知数列{an}满足a1=1,an+1an+Sn=5,则a2=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
11.已知平面向量$\overrightarrow a=(-2,1)$,$\overrightarrow b=(1,2)$,则$|{\overrightarrow a-2\overrightarrow b}|$的值是( )
| A. | 1 | B. | 5 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
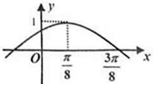 函数f(x)=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的单调递减区间为[$\frac{π}{4}+kπ$,$\frac{5π}{8}+kπ$],k∈Z.
函数f(x)=sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的单调递减区间为[$\frac{π}{4}+kπ$,$\frac{5π}{8}+kπ$],k∈Z.