函数f(x∈R.ω＞0.-π≤φ＜π)的部分图象如图所示.则( )A．ω=$\frac{π}{2}$.φ=-πB．ω=$\frac{π}{2}$.φ=0C．ω=$\frac{π}{4}$.φ=$\frac{π}{4}$D．ω=$\frac{π}{4}$.φ=-$\frac{3π}{4}$ 题目和参考答案——青夏教育精英家教网—

题目内容

7．函数f（x）=sin（ωx+φ）（x∈R，ω＞0，-π≤φ＜π）的部分图象如图所示，则（　　）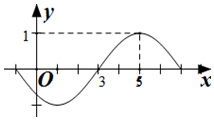

A．

ω=$\frac{π}{2}$，φ=-π

B．

ω=$\frac{π}{2}$，φ=0

C．

ω=$\frac{π}{4}$，φ=$\frac{π}{4}$

D．

ω=$\frac{π}{4}$，φ=-$\frac{3π}{4}$

分析利用周期求出ω，利用最高点求出φ的值．

解答解：由题意，T=8=$\frac{2π}{ω}$，∴ω=$\frac{π}{4}$，
∵f（5）=sin（$\frac{5}{4}$π+φ）=1，-π≤φ＜π
∴φ=-$\frac{3π}{4}$，
故选D．

点评本题考查三角函数的图象，考查函数解析式的求解，比较基础．

练习册系列答案

18．已知数列{a_n}的前n项和${S_n}=-{a_n}-{（\frac{1}{2}）^{n-1}}+2$（n∈N^*），则数列{a_n}的通项公式a_n=$\frac{n}{{2}^{n}}$．

15．设函数$f（x）=2cosx（cos+\sqrt{3}sinx）$（x∈R）．
（1）求函数y=f（x）的周期和单调递增区间；
（2）当$x∈[0，\frac{π}{2}]$时，求函数f（x）的最大值．

2．直线MN的斜率为2，其中点N（1，-1），点M在直线y=x+1上，则（　　）

12．已知数列{a_n}满足a₁=1，a_n+1=$\left\{\begin{array}{l}{{a}_{n}+1，{a}_{n}＜3}\\{\frac{{a}_{n}}{3}，{a}_{n}≥3}\end{array}\right.$，则数列{a_n}的前12项和S₁₂=24．

19．设集合U={0，1，2，3，4，5}，A={1，2，3}，B={x∈Z|x²-5x+4≥0}，则A∩（∁_UB）=（　　）

16．已知f（x）是定义在R上的可导函数，且满足（x+2）f（x）+xf'（x）＞0，则（　　）

17．若${（{{x^2}+\frac{a}{x}}）^n}$的展开式中，二项式系数和为64，所有项的系数和为729，则a的值为-4或2．

试题分类