题目内容
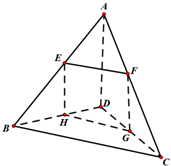 如图,空间四边形被一平面所截,截面EFGH是平行四边形.求证:
如图,空间四边形被一平面所截,截面EFGH是平行四边形.求证:(1)EF∥平面BCD;
(2)BC∥平面EFGH.
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)(2)根据线面平行的判定定理进行证明即可.
解答:
解:(1)∵四边形EFGH是平行四边形,
∴EF∥HG,
∵EF?平面BCD,HG?平面BCD,
∴EF∥平面BCD;
(2)由(1)得:EF∥平面BCD,
∴BC∥EF,
∵BC?平面EFGH,EF?平面EFGH,
∴BC∥平面EFGH.
∴EF∥HG,
∵EF?平面BCD,HG?平面BCD,
∴EF∥平面BCD;
(2)由(1)得:EF∥平面BCD,
∴BC∥EF,
∵BC?平面EFGH,EF?平面EFGH,
∴BC∥平面EFGH.
点评:本题考查了线面平行的判定定理,考查了平行四边形的性质,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知-
<θ<0,且sinθ+cosθ=a,其中a∈(0,1),则关于tanθ的值,在以下四个答案中,可能正确的是( )
| π |
| 2 |
A、-
| ||
| B、-3 | ||
C、-
| ||
D、
|
正方体ABCD-A′B′C′D′中,异面直线AB′和A′D所成角为( )
| A、45° | B、60° |
| C、90° | D、60°或120° |
线面角与二面角的取值范围分别是( )
A、[0,
| ||
B、[0,
| ||
C、[0,
| ||
D、[0,
|
设f(x)是R上的偶函数,且在[0,+∞)上递增,若f(
)=0,f(log
x)<0,那么x的取值范围是( )
| 1 |
| 2 |
| 1 |
| 4 |
A、
| ||
| B、x>2 | ||
C、
| ||
D、x>2或
|
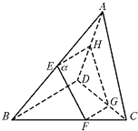 如图,空间四边形ABCD中,E、F、G分别是AB、BC、CD上,且满足AE:EB=CF:FB=2:1,CG:GD=3:1,过E、F、G的平面交AD于点H.
如图,空间四边形ABCD中,E、F、G分别是AB、BC、CD上,且满足AE:EB=CF:FB=2:1,CG:GD=3:1,过E、F、G的平面交AD于点H.