题目内容
7.求证:$\frac{1+sinα-cosα}{1+sinα+cosα}$=$\frac{1-cosα}{sinα}$.分析 利用三角函数的恒等变换,分别化简等式的左边与右边,即可证明等式成立.
解答 证明:左边=$\frac{1+sinα-cosα}{1+sinα+cosα}$=$\frac{(1-cosα)+sinα}{(1+cosα)+sinα}$=$\frac{{2sin}^{2}\frac{α}{2}+2sin\frac{α}{2}cos\frac{α}{2}}{{2cos}^{2}\frac{α}{2}+2sin\frac{α}{2}cos\frac{α}{2}}$=$\frac{sin\frac{α}{2}}{cos\frac{α}{2}}$=tan$\frac{α}{2}$,
右边=$\frac{1-cosα}{sinα}$=$\frac{{2sin}^{2}\frac{α}{2}}{2sin\frac{α}{2}cos\frac{α}{2}}$=$\frac{sin\frac{α}{2}}{cos\frac{α}{2}}$=tan$\frac{α}{2}$,
∴左边=右边,等式成立.
点评 本题考查了三角函数恒等式的证明问题,是基础题目.

练习册系列答案
相关题目
2.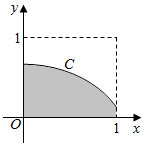 在如图所示的正方形中随机投掷10000个点,则落入阴影外部(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影外部(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
附:若X~N(μ,σ2),则P(μ-δ<X≤μ+δ)=0.6826,P(μ-2δ<X≤μ+2δ)=0.9544.
 在如图所示的正方形中随机投掷10000个点,则落入阴影外部(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影外部(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )附:若X~N(μ,σ2),则P(μ-δ<X≤μ+δ)=0.6826,P(μ-2δ<X≤μ+2δ)=0.9544.
| A. | 3413 | B. | 1193 | C. | 2718 | D. | 6587 |
19.直线x-$\sqrt{3}$y+1=0的倾斜角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
17.如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$的共轭复数是( )


| A. | i | B. | -i | C. | $\frac{3}{5}$i | D. | -$\frac{3}{5}$i |