题目内容

2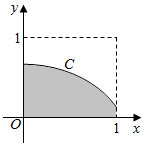．在如图所示的正方形中随机投掷10000个点，则落入阴影外部（曲线C为正态分布N（0，1）的密度曲线）的点的个数的估计值为（　　）
附：若X～N（μ，σ2），则P（μ-δ＜X≤μ+δ）=0.6826，P（μ-2δ＜X≤μ+2δ）=0.9544．
A．3413B．1193C．2718D．6587

分析 求出P（0＜X≤1）=$\frac{1}{2}$×0.6826=0.3413，即可得出落入阴影外部（曲线C为正态分布N（0，1）的密度曲线）的点的个数的估计值．

解答 解：由题意P（0＜X≤1）=$\frac{1}{2}$×0.6826=0.3413，
∴落入阴影部分点的个数的估计值为10000×0.3413=3413，
∴落入阴影外部（曲线C为正态分布N（0，1）的密度曲线）的点的个数的估计值为10000-3413=6587．
故选：D．

点评 本题考查正态分布曲线的特点及曲线所表示的意义，考查正态分布中两个量μ和σ的应用，考查曲线的对称性，属于基础题．

练习册系列答案
相关题目
18．已知函数y=f（x）满足f（2x）=2f（x），当1≤x≤2时，f（x）=$\frac{1}{2}$-|x-$\frac{3}{2}$|，当x∈[1，2n]，n∈N*时，函数y=f（x）的图象与x轴所围成的图形面积记为Sn，则S1=$\frac{1}{4}$，Sn=$\frac{1}{12}$（4n-1）．
19．函数f（x）=1+$\frac{sinx}{2+cosx}$的最大值与最小值之和为2．
10．已知函数f（x）=sinx+cosx，x∈R．
（Ⅰ）求f（$\frac{π}{2}$）的值；
（Ⅱ）求函数f（x）的最小正周期；
（Ⅲ）求函数g（x）=f（x+$\frac{π}{4}$）+f（x+$\frac{3π}{4}$）的最小值．
17．过直线l：x+y=2上任意点P向圆C：x2+y2=1作两条切线，切点分别为A，B，线段AB的中点为Q，则点Q到直线l的距离的取值范围为[$\frac{\sqrt{2}}{2}$，$\sqrt{2}$）．
7．求证：$\frac{1+sinα-cosα}{1+sinα+cosα}$=$\frac{1-cosα}{sinα}$．
14．某地市高三理科学生有15000名，在一次调研测试中，数学成绩ξ服从正态分布N（100，σ2），已知P（80＜ξ≤100）=0.40，若按成绩分层抽样的方式取100份试卷进行分析，则应从120分以上的试卷中抽取（　　）
A．5份B．10份C．15份D．20份
11．已知圆C1：（x+2）2+（y-3）2=1，圆C2：（x-3）2+（y-4）2=9，A，B分别是圆C1和圆C2上的动点，点P是y轴上的动点，则|PB|-|PA|的最大值为（　　）
A．$\sqrt{2}$+4B．5$\sqrt{2}-4$C．$\sqrt{2}$D．$\sqrt{26}$
12．在△ABC中，角A，B，C的对边分别为a，b，c，已知a=2，bcosC-ccosB=4，$\frac{π}{4}$≤C≤$\frac{π}{3}$，则tanA的最大值为$\frac{1}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网