题目内容
已知集合M={x|
≥0},N={x|(x-1)(x+1)≥0},P={x|2(x-1)(x+2)≥
},则M,N,P之间的关系是( )
| x-1 |
| x+2 |
| 1 |
| 4 |
| A、P?M=N |
| B、P?M?N |
| C、M?N?P |
| D、M=N?P |
考点:集合的包含关系判断及应用
专题:计算题,集合
分析:化简集合M,N,P.
解答:
解:M={x|
≥0}={x|x<-2或x≥1},
N={x|(x-1)(x+1)≥0}={x|x≤-1或x≥1},
P={x|2(x-1)(x+2)≥
}={x|x≤-1或x≥0},
故M?N?P.
故选:C.
| x-1 |
| x+2 |
N={x|(x-1)(x+1)≥0}={x|x≤-1或x≥1},
P={x|2(x-1)(x+2)≥
| 1 |
| 4 |
故M?N?P.
故选:C.
点评:考查了集合间相互关系的判定及不等式的解法.

练习册系列答案
相关题目
下列四个关系中,正确的是( )
| A、a∈{a,b} |
| B、{a}∈{a,b} |
| C、a∉{a} |
| D、a∉{a,b} |
 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为( )A、6
| ||
B、4
| ||
| C、6 | ||
| D、4 |
已知函数f(x)=3x3+2x,则f(2)=( )
| A、10 | B、28 | C、31 | D、18 |
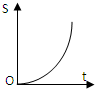
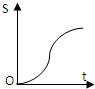
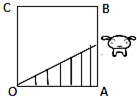 如图,正方形街道OABC,已知小白从A出发,沿着正方形边缘A-B-C匀速走动,小白与O连线扫过的正方形内阴影部分面积S是时间t的函数,这个函数的大致图象是( )
如图,正方形街道OABC,已知小白从A出发,沿着正方形边缘A-B-C匀速走动,小白与O连线扫过的正方形内阴影部分面积S是时间t的函数,这个函数的大致图象是( )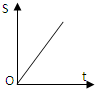
 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.