题目内容
15.已知P是△ABC内一点,且满足2$\overrightarrow{PA}$+3$\overrightarrow{PB}$+4$\overrightarrow{PC}$=$\overrightarrow{0}$,那么S△PBC:SPCA:S△PAB等于( )| A. | 4:3:2 | B. | 2:3:4 | C. | $\frac{1}{4}$:$\frac{1}{3}$:$\frac{1}{2}$ | D. | $\frac{1}{2}$:$\frac{1}{3}$:$\frac{1}{4}$ |
分析 由已知得$\overrightarrow{PA}+\frac{3}{2}\overrightarrow{PB}+2\overrightarrow{PC}=\overrightarrow{0}$.延长PB到B1,使得$\overrightarrow{P{B}_{1}}=\frac{3}{2}\overrightarrow{PB}$,延长PC到C1,使得$\overrightarrow{P{C}_{1}}=2\overrightarrow{PC}$,则P是△PB1C1的重心,设${S}_{△P{B}_{1}{C}_{1}}$=3S,则${S}_{△AP{B}_{1}}={S}_{△AP{C}_{1}}={S}_{△P{B}_{1}{C}_{1}}$=S,由此能求出S△PBC:S△PCA:S△PAB的值.
解答 解: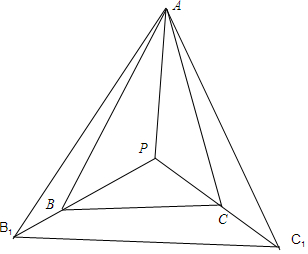 ∵P是△ABC内一点,且满足2$\overrightarrow{PA}$+3$\overrightarrow{PB}$+4$\overrightarrow{PC}$=$\overrightarrow{0}$,
∵P是△ABC内一点,且满足2$\overrightarrow{PA}$+3$\overrightarrow{PB}$+4$\overrightarrow{PC}$=$\overrightarrow{0}$,
∴$\overrightarrow{PA}+\frac{3}{2}\overrightarrow{PB}+2\overrightarrow{PC}=\overrightarrow{0}$.
延长PB到B1,使得$\overrightarrow{P{B}_{1}}=\frac{3}{2}\overrightarrow{PB}$,延长PC到C1,使得$\overrightarrow{P{C}_{1}}=2\overrightarrow{PC}$,
连结PB1、PC1、B1C1,则$\overrightarrow{PA}+\overrightarrow{P{B}_{1}}+\overrightarrow{P{C}_{1}}=\overrightarrow{0}$.
∴P是△PB1C1的重心,
设${S}_{△P{B}_{1}{C}_{1}}$=3S,则${S}_{△AP{B}_{1}}={S}_{△AP{C}_{1}}={S}_{△P{B}_{1}{C}_{1}}$=S,
${S}_{△PBC}=\frac{2}{3}×\frac{1}{2}×S=\frac{1}{3}S$,
S△PCA=$\frac{1}{2}S$,S△PAB=$\frac{2}{3}S$,
∴S△PBC:S△PCA:S△PAB=$\frac{1}{3}S:\frac{1}{2}S:\frac{2}{3}S$=2:3:4.
故选:B.
点评 本题考查三个三角形面积之比的求法,考查向量、三角形重心定理等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想,是中档题.

| A. | p是真命题且q是假命题 | B. | p是真命题且q是真命题 | ||
| C. | p是假命题且q是真命题 | D. | p是真命题且q是假命题 |
| A. | (-∞,lge-lg(lge)] | B. | (-∞,1] | C. | [1,lge-lg(lge)] | D. | [lge-lg(lge),+∞) |
| A. | [$\frac{1}{2}$,1) | B. | [$\frac{\sqrt{2}}{2},\frac{\sqrt{3}}{2}$] | C. | [$\frac{\sqrt{2}}{2}$,1] | D. | [$\frac{\sqrt{3}}{2}$,1) |

| A. | 24 | B. | 30 | C. | 48 | D. | 72 |
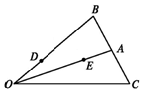 已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近O的三等分点,设$\overrightarrow{OB}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$
已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近O的三等分点,设$\overrightarrow{OB}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$