题目内容
4.用反证法证明“若函数f(x)=x2+px+q.则|f(1)|,|f(2)|,|f(3)|中至少有一个不小于$\frac{1}{2}$”时,假设内容是f(1)|,|f(2)|,|f(3)|都小于$\frac{1}{2}$..分析 用反证法证明数学命题时,应先假设要证的结论的反面成立,即命题的否定.
解答 解:用反证法证明数学命题时,应先假设要证的结论的反面成立,
而“|f(1)|,|f(2)|,|f(3)|至少有一个不小于$\frac{1}{2}$”的否定为:|f(1)|,|f(2)|,|f(3)|都小于$\frac{1}{2}$,
故答案为f(1)|,|f(2)|,|f(3)|都小于$\frac{1}{2}$.
点评 本题主要考查命题的否定,用反证法证明数学命题的方法和步骤,把要证的结论进行否定,得到要证的结论的反面,是解题的突破口,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
15.已知P是△ABC内一点,且满足2$\overrightarrow{PA}$+3$\overrightarrow{PB}$+4$\overrightarrow{PC}$=$\overrightarrow{0}$,那么S△PBC:SPCA:S△PAB等于( )
| A. | 4:3:2 | B. | 2:3:4 | C. | $\frac{1}{4}$:$\frac{1}{3}$:$\frac{1}{2}$ | D. | $\frac{1}{2}$:$\frac{1}{3}$:$\frac{1}{4}$ |
9.函数$f(x)=\frac{x^3}{3}+\frac{1}{x}$的导数f'(x)=( )
| A. | $\frac{x^2}{3}+\frac{1}{x}$ | B. | ${x^2}-\frac{1}{x^2}$ | C. | $-{x^2}-\frac{1}{x^2}$ | D. | x2+lnx |
16.某中学将100名高二文科生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲、乙两个班进行教改实验.为了了解教学效果,期末考试后,陈老师对甲、乙两个班级的学生成绩进行统计分析,画出频率分布直方图(如图).记成绩不低于90分者为“成绩优秀”.
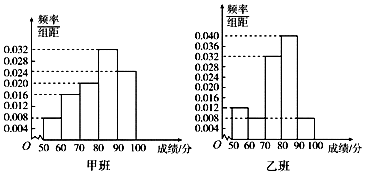
(Ⅰ)根据频率分布直方图填写下面2×2列联表;
(Ⅱ)判断能否在犯错误的概率不超过0.05的前提下认为:“成绩优秀”与教学方式有关?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.

(Ⅰ)根据频率分布直方图填写下面2×2列联表;
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | 12 | 4 | 20 |
| 成绩不优秀 | 38 | 46 | 80 |
| 总计 | 50 | 50 | 100 |
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
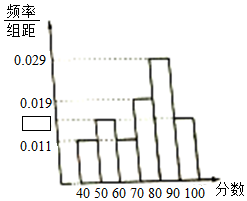 为了解某社区物业部门对本小区业主的服务情况,随机访问了100位业主,根据这100位业主对物业部门的评分情况,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].由于某种原因,有个数据出现污损,请根据图中其他数据分析,评分不小于80分的业主有( )位.
为了解某社区物业部门对本小区业主的服务情况,随机访问了100位业主,根据这100位业主对物业部门的评分情况,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].由于某种原因,有个数据出现污损,请根据图中其他数据分析,评分不小于80分的业主有( )位.