题目内容
20.设p,q是两个命题,若(¬p)∧q是真命题,那么( )| A. | p是真命题且q是假命题 | B. | p是真命题且q是真命题 | ||
| C. | p是假命题且q是真命题 | D. | p是真命题且q是假命题 |
分析 由题意得到(?p)和q都是真命题,由此能求出p是假命题且q是真命题.
解答 解:∵p,q是两个命题,(¬p)∧q是真命题,
∴(?p)和q都是真命题,
∴p是假命题且q是真命题.
故选:C.
点评 本题考查命题的真假判断,是基础题,解题时要认真审,注意复合命题的性质的合理运用.

练习册系列答案
相关题目
10.函数f(x)=lnx-x的单调增区间为( )
| A. | (1,+∞) | B. | (0,1) | C. | (-∞,1) | D. | (0,+∞) |
15.(文)已知定义在实数集R上的函数f(x)满足f(2)=7,且f(x)的导数f′(x)在R上恒有f′(x)<3(x∈R),则不等式f(x)<3x+1的解集为( )
| A. | (1,+∞) | B. | (-∞,-2) | C. | (-∞.-1)∪(1,+∞) | D. | (2,+∞) |
5.若关于x不等式xlnx-x3+x2≤aex恒成立,则实数a的取值范围是( )
| A. | [e,+∞) | B. | [0,+∞) | C. | $[\frac{1}{e},+∞)$ | D. | [1,+∞) |
15.已知P是△ABC内一点,且满足2$\overrightarrow{PA}$+3$\overrightarrow{PB}$+4$\overrightarrow{PC}$=$\overrightarrow{0}$,那么S△PBC:SPCA:S△PAB等于( )
| A. | 4:3:2 | B. | 2:3:4 | C. | $\frac{1}{4}$:$\frac{1}{3}$:$\frac{1}{2}$ | D. | $\frac{1}{2}$:$\frac{1}{3}$:$\frac{1}{4}$ |
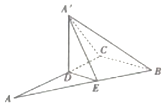 如图,将直角△ABC沿着平行BC边的直线DE折起,使得平面A′DE⊥平面BCDE,其中D、E分别在AC、AB边上,且AC⊥BC,BC=3,AB=5,点A′为点A折后对应的点,当四棱锥A′-BCDE的体积取得最大值时,求AD的长.
如图,将直角△ABC沿着平行BC边的直线DE折起,使得平面A′DE⊥平面BCDE,其中D、E分别在AC、AB边上,且AC⊥BC,BC=3,AB=5,点A′为点A折后对应的点,当四棱锥A′-BCDE的体积取得最大值时,求AD的长.