题目内容

20．已知集合A={x|y=lg（3-2x）}，B={x|x2≤4}，则A∪B=（　　）
A．$\{\left.x\right|-2≤x＜\frac{3}{2}\}$B．{x|x＜2}C．$\{\left.x\right|-2＜x＜\frac{3}{2}\}$D．{x|x≤2}

分析 先分别求出集合A和B，由此能求出A∪B．

解答 解：因为$A=\{\left.x\right|y=lg（3-2x）\}=\{\left.x\right|3-2x＞0\}=\{\left.x\right|x＜\frac{3}{2}\}$，
B={x|x2≤4}={x|-2≤x≤2}．
所以A∪B={x|x≤2}．
故答案为：D．

点评 本题考查并集的求法，是基础题，解题时要认真审题，注意并集定义的合理运用．

练习册系列答案
相关题目
10．$\frac{1-i}{1+i}$=（　　）
A．-iB．iC．1D．-1
11．已知函数f（x）=sinωx+$\sqrt{3}$cosωx（ω＞0）在（$\frac{π}{6}$，$\frac{π}{2}$）上单调，且满足f（$\frac{π}{6}$）+f（$\frac{π}{2}$）=0，则ω=（　　）
A．2B．3C．4D．5
8．已知点F（3，0）是双曲线3x2-my2=3m（m＞0）的一个焦点，则此双曲线的离心率为$\frac{\sqrt{6}}{2}$．
15．已知A，B为抛物线E：y2=2px（p＞0）上异于顶点O的两点，△AOB是等边三角形，其面积为48$\sqrt{3}$，则p的值为（　　）
A．2B．2$\sqrt{3}$C．4D．4$\sqrt{3}$
5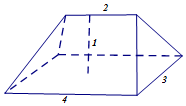．《九章算术》卷第五《商功》中，有问题“今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高一丈．问积几何？”，意思是：“今有底面为矩形的屋脊状的楔体，下底面宽3丈，长4丈；上棱长2丈，无宽，高1丈（如图）．
问它的体积是多少？”这个问题的答案是（　　）
A．5立方丈B．6立方丈C．7立方丈D．9立方丈
12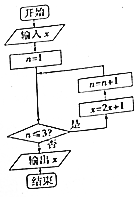．阅读右边程序框图，当输入的值为3时，运行相应程序，则输出x的值为（　　）
A．7B．15C．31D．63
9．已知函数f（x）=sinx-x，则不等式f（x+2）+f（1-2x）＜0的解集是（　　）
A．$（-∞，-\frac{1}{3}）$B．$（-\frac{1}{3}，+∞）$C．（3，+∞）D．（-∞，3）
10．对于定义在[0，+∞）上的函数f（x），如果同时满足下列三条：
①对任意的x∈[0，+∞），总有f（x）≥0；
②若x1≥0，x2≥0，都有f（x1+x2）≥f（x1）+f（x2）成立；
③若0≤x1＜x2＜1，则$\frac{{f（{x_1}+1）-f（{x_2}+1）}}{{{x_1}-{x_2}}}$＞1．
则称函数f（x）为超级囧函数，则下列是超级囧函数的为（3）．
（1）f（x）=sinx
（2）g（x）=$\frac{1}{4}{x^2}$（x∈[0，1]）
（3）h（x）=2x-1；
（4）p（x）=ln（x+1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网