题目内容
9.已知A为△ABC的最小内角,若向量$\overrightarrow{a}$=(cos2A,sin2A),$\overrightarrow{b}$=($\frac{1}{co{s}^{2}A+1}$,$\frac{1}{si{n}^{2}A-2}$),则$\overrightarrow{a}$$•\overrightarrow{b}$的取值范围是( )| A. | (-∞,$\frac{1}{2}$) | B. | (-1,$\frac{1}{2}$) | C. | [-$\frac{2}{5}$,$\frac{1}{2}$) | D. | [-$\frac{2}{5}$,+∞) |
分析 利用向量的数量积得出$\overrightarrow{a}$$•\overrightarrow{b}$=cos2A•$\frac{1}{co{s}^{2}A+1}$+sin2A•$\frac{1}{si{n}^{2}A-2}$=2+$\frac{3}{si{n}^{2}A-2}$,A∈(0,$\frac{π}{3}$],再利用单调性求解即可.
解答 解:∵A为△ABC的最小内角,若向量$\overrightarrow{a}$=(cos2A,sin2A),$\overrightarrow{b}$=($\frac{1}{co{s}^{2}A+1}$,$\frac{1}{si{n}^{2}A-2}$),
∴$\overrightarrow{a}$$•\overrightarrow{b}$=cos2A•$\frac{1}{co{s}^{2}A+1}$+sin2A•$\frac{1}{si{n}^{2}A-2}$=2+$\frac{3}{si{n}^{2}A-2}$,A∈(0,$\frac{π}{3}$]
根据函数解析式判断为减函数
∴最大值为:2-$\frac{3}{2}$=$\frac{1}{2}$,(此值取不着)
最小值为:2$+\frac{3}{\frac{3}{4}-2}$=$-\frac{2}{5}$
∴$\overrightarrow{a}$$•\overrightarrow{b}$的取值范围[$-\frac{2}{5}$,$\frac{1}{2}$)
故选:C
点评 本题考查了三角形的性质,平面向量的运算,性质,三角函数的单调性的运用,属于综合题目.

练习册系列答案
相关题目
19.命题p:?x∈N,x3<x2;命题q:?a∈(0,1)∪(1,+∞),函数f(x)=loga(x-1)的图象过点(2,0),则下列命题是真命题的是( )
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
4.已知i为虚数单位,若复数i•z=$\sqrt{2}$-i,则|z|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
9.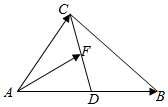 如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}+\frac{4}{y+1}$的最小值为( )
如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}+\frac{4}{y+1}$的最小值为( )
 如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}+\frac{4}{y+1}$的最小值为( )
如图所示,在△ABC中,AD=DB,点F在线段CD上,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{AF}=x$$\overrightarrow{a}$+y$\overrightarrow{b}$,则$\frac{1}{x}+\frac{4}{y+1}$的最小值为( )| A. | $6+2\sqrt{2}$ | B. | $6\sqrt{3}$ | C. | 6+4$\sqrt{2}$ | D. | $3+2\sqrt{2}$ |