题目内容
8．已知函数f（x）=$\left\{\begin{array}{l}{{e}^{x+2}，x≤0}\\{lnx，x＞0}\end{array}\right.$，则f（f（-3）=）-1．分析 利用分布函数性质求解．
解答 解：∵f（x）=$\left\{\begin{array}{l}{{e}^{x+2}，x≤0}\\{lnx，x＞0}\end{array}\right.$，
∴f（-3）=e-3+2=e-1，
f（f（-3）=f（e-1）=lne-1=-1．
故答案为：-1．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意分段函数的性质的合理运用．
练习册系列答案
相关题目
3．与向量$\overrightarrow{a}$=（6，8）共线的单位向量是（ ）
| A． | （-$\frac{3}{5}$，-$\frac{4}{5}$） | B． | （0，1） | C． | （3，4） | D． | （$\frac{4}{5}$，$\frac{3}{5}$） |
19．命题p：?x∈N，x3＜x2；命题q：?a∈（0，1）∪（1，+∞），函数f（x）=loga（x-1）的图象过点（2，0），则下列命题是真命题的是（ ）
| A． | p∧q | B． | p∧￢q | C． | ￢p∧q | D． | ￢p∧￢q |
3．已知cos（α+$\frac{π}{2}$）=$\frac{1}{3}$，则cos2α的值等于（ ）
| A． | $\frac{7}{9}$ | B． | -$\frac{7}{9}$ | C． | $\frac{8}{9}$ | D． | -$\frac{8}{9}$ |
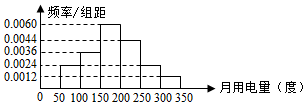为了了解长沙市居民月用电情况，抽查了该市100户居民用电量（单位：度），得到频率分布直方图如下：根据如图可得到这100户居民月用电量在[150，300]的用户数是（ ）