题目内容
已知⊙C:(x-2)2+(y-1)2=4,直线l:y=-x+1,则l被⊙C所截得的弦长为( )
A、2
| ||
| B、2 | ||
C、
| ||
| D、1 |
考点:直线与圆相交的性质
专题:计算题,直线与圆
分析:确定圆的圆心、半径,求得圆心(2,1)到直线l:y=-x+1的距离,再根据弦长等于2
,计算求得结果.
| r2-d2 |
解答:
解:圆C:(x-2)2+(y-1)2=4的圆心坐标为(2,1),半径为r=2,
圆心(2,1)到直线l:y=-x+1的距离为d=
=
,
故弦长等于2
=2
,
故选:A.
圆心(2,1)到直线l:y=-x+1的距离为d=
| 2 | ||
|
| 2 |
故弦长等于2
| r2-d2 |
| 2 |
故选:A.
点评:本题主要考查直线和圆相交的性质,点到直线的距离公式、弦长公式的应用,属于中档题.

练习册系列答案
相关题目
下列说法正确的是( )
A、甲掷硬币10次,正面向上3次,则正面向上的概率为
| ||
B、某种彩票中奖的概率为
| ||
C、某地天气预报说明天下雨的概率是
| ||
D、掷一颗骰子一次得到3向上的概率为
|
设向量
=(2,t)与向量
=(1,3)共线,则t等于( )
| a |
| b |
| A、-6 | ||
B、
| ||
C、
| ||
| D、6 |
在四边形ABCD中,
-
+
等于( )
| AB |
| AC |
| BD |
A、
| ||
B、
| ||
C、
| ||
D、
|
2log510+log50.25+(
)-2=( )
| 1 |
| 2 |
| A、2 | B、4 | C、6 | D、8 |
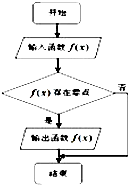 执行如图所示的程序框图,若输入如下四个函数:
执行如图所示的程序框图,若输入如下四个函数: