题目内容
16.若A为△ABC的一个内角,且sinA+cosA=$\frac{1}{5}$,则A=( )| A. | arcsin$\frac{4}{5}$ | B. | arcsin(-$\frac{4}{5}$) | C. | $\frac{π}{2}$+arcsin$\frac{4}{5}$ | D. | $\frac{π}{2}$+arccos$\frac{4}{5}$ |
分析 由条件利用同角三角函数的基本关系,三角函数在各个象限中的符号,求得tanA的值,进而可求cosA,sinA,利用A的范围及sinA的值,即可计算得解.
解答 解:(1)∵A为△ABC的一个内角,cosA+sinA=$\frac{1}{5}$,平方可得1+2sinAcosA=$\frac{1}{25}$,
即sinAcosA=-$\frac{12}{25}$,∴sinA>0,cosA<0,|sinA|>|cosA|,tanA<-1.
再根据 $\frac{sinAcosA}{si{n}^{2}A+co{s}^{2}A}$=$\frac{tanA}{ta{n}^{2}A+1}$,求得tanA=-$\frac{4}{3}$,或tanA=-$\frac{3}{4}$(舍去).
∴cosA=-$\sqrt{\frac{1}{1+ta{n}^{2}A}}$=-$\frac{3}{5}$,sinA=$\sqrt{1-co{s}^{2}A}$=$\frac{4}{5}$,
∵sin($\frac{π}{2}$+arccos$\frac{4}{5}$)=$\frac{4}{5}$,且$\frac{π}{2}$+arccos$\frac{4}{5}$∈($\frac{π}{2}$,π),
∴A=$\frac{π}{2}$+arccos$\frac{4}{5}$.
故选:D.
点评 本题主要考查同角三角函数的基本关系,三角函数在各个象限中的符号,属于基础题.

练习册系列答案
相关题目
11.已知向量$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(0,1),则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=( )
| A. | 2$\sqrt{2}$ | B. | $\sqrt{5}$ | C. | 2 | D. | 4 |
1.已知$\overrightarrow{a}$=2,$\overrightarrow{b}$=1,$\overrightarrow{a}$•($\overrightarrow{a}$+$\overrightarrow{b}$)=5,则$\overrightarrow{a}$,$\overrightarrow{b}$夹角的余弦值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2\sqrt{3}}{5}$ | D. | $\frac{\sqrt{2}}{2}$ |
5.函数y=3cosx是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
19.六个人站成一排照相,则甲、乙两人之间恰好站两人的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
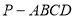 中,
中,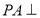 平面
平面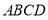 ,底面
,底面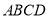 是直角梯形,且
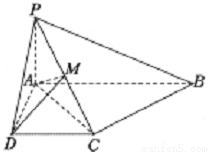
是直角梯形,且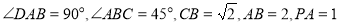 .
.
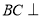 平面
平面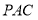 ;
;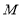 是
是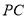 的中点,求三棱锥
的中点,求三棱锥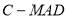 的体积.
的体积.