题目内容
19.六个人站成一排照相,则甲、乙两人之间恰好站两人的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
分析 六个人站成一排照相,先求出基本事件总数,再求出甲、乙两人之间恰好站两人包含基本事件个数,由此能求出甲、乙两人之间恰好站两人的概率.
解答 解:六个人站成一排照相,基本事件总数n=${A}_{6}^{6}$=720,
甲、乙两人之间恰好站两人包含基本事件个数m=${A}_{2}^{2}{A}_{4}^{2}{A}_{3}^{3}$=144,
∴甲、乙两人之间恰好站两人的概率p=$\frac{m}{n}$=$\frac{144}{720}$=$\frac{1}{5}$.
故选:B.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
16.若A为△ABC的一个内角,且sinA+cosA=$\frac{1}{5}$,则A=( )
| A. | arcsin$\frac{4}{5}$ | B. | arcsin(-$\frac{4}{5}$) | C. | $\frac{π}{2}$+arcsin$\frac{4}{5}$ | D. | $\frac{π}{2}$+arccos$\frac{4}{5}$ |
14.设O是△ABC的外接圆圆心,且$\overrightarrow{OA}+\sqrt{3}\overrightarrow{OB}+2\overrightarrow{OC}=\overrightarrow 0$,则∠AOC=( )
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{5π}{6}$ |
11.已知函数f(x)满足f(x)+f(2-x)=2,当x∈(0,1]时,f(x)=x2,当x∈(-1,0]时,$f(x)+2=\frac{2}{{f(\sqrt{x+1})}}$,若定义在(-1,3)上的函数g(x)=f(x)-t(x+1)有三个不同的零点,则实数t的取值范围是( )
| A. | $(0,\frac{1}{2}]$ | B. | $[\frac{1}{2},+∞)$ | C. | $(0,6+2\sqrt{7})$ | D. | $(0,6-2\sqrt{7})$ |
8.平面直角坐标系xOy中,已知向量$\overrightarrow{OA}$与$\overrightarrow{OB}$关于y轴对称,向量$\overrightarrow{a}$=(1,0),则满足$\overrightarrow{O{A}^{2}}$+$\overrightarrow{a}$$•\overrightarrow{AB}$=0的点A(x,y)的轨迹方程为( )
| A. | (x+1)2+y2=1 | B. | (x-1)2+y2=1 | C. | x2+y2=1 | D. | x2+(y-1)2=1 |
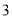 ,且每个顶点都在球
,且每个顶点都在球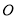 的表面上,则球
的表面上,则球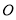 的半径为( )
的半径为( )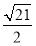 B.
B.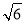 C.
C.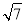 D.
D.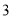
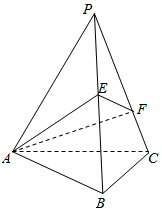 如图,已知正三棱锥P-ABC的底面边长为4,侧棱长为8,E、F分别为PB、PC上的动点,求截面△AEF周长的最小值,并求出此时三棱锥P-AEF的体积.
如图,已知正三棱锥P-ABC的底面边长为4,侧棱长为8,E、F分别为PB、PC上的动点,求截面△AEF周长的最小值,并求出此时三棱锥P-AEF的体积.