题目内容
5.函数y=3cosx是( )| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
分析 由奇偶性的定义和诱导公式可判.
解答 解:∵y=f(x)=3cosx,
∴f(-x)=3cos(-x)=3cosx=f(x),
∴函数y=3cosx是偶函数.
故选:B.
点评 本题考查余弦函数的奇偶性,属基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
16.若A为△ABC的一个内角,且sinA+cosA=$\frac{1}{5}$,则A=( )
| A. | arcsin$\frac{4}{5}$ | B. | arcsin(-$\frac{4}{5}$) | C. | $\frac{π}{2}$+arcsin$\frac{4}{5}$ | D. | $\frac{π}{2}$+arccos$\frac{4}{5}$ |
10.已知tna2α=-$\frac{4}{3}$,α是第一象限角,则tanα等于( )
| A. | 1 | B. | 3 | C. | 4 | D. | 2 |
8.平面直角坐标系xOy中,已知向量$\overrightarrow{OA}$与$\overrightarrow{OB}$关于y轴对称,向量$\overrightarrow{a}$=(1,0),则满足$\overrightarrow{O{A}^{2}}$+$\overrightarrow{a}$$•\overrightarrow{AB}$=0的点A(x,y)的轨迹方程为( )
| A. | (x+1)2+y2=1 | B. | (x-1)2+y2=1 | C. | x2+y2=1 | D. | x2+(y-1)2=1 |
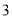 ,且每个顶点都在球
,且每个顶点都在球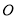 的表面上,则球
的表面上,则球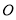 的半径为( )
的半径为( )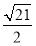 B.
B.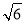 C.
C.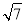 D.
D.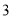
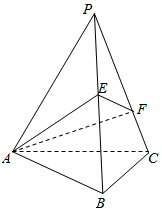 如图,已知正三棱锥P-ABC的底面边长为4,侧棱长为8,E、F分别为PB、PC上的动点,求截面△AEF周长的最小值,并求出此时三棱锥P-AEF的体积.
如图,已知正三棱锥P-ABC的底面边长为4,侧棱长为8,E、F分别为PB、PC上的动点,求截面△AEF周长的最小值,并求出此时三棱锥P-AEF的体积.