题目内容
已知
=（cosα，1，sinα），
=（sinα，1，cosα），且sinα≠cosα，则向量
+
与
-
的夹角是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、0° | B、30° |
| C、60° | D、90° |
考点：平面向量数量积的运算
专题：高考数学专题,空间向量及应用
分析：根据向量的数量积，得到（
+
）•（
-
）=0，继而得到
+
⊥
-
，故向量
+
与
-
的夹角是90°
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
解答：
解：∵
=（cosα，1，sinα），
=（sinα，1，cosα），
∴（
+
）•（
-
）=
2-
2=cos2α+1+sin2α-（sin2α+1+cos2α）=0，
∵sinα≠cosα，
∴（
+
）⊥（
-
）
故向量
+
与
-
的夹角是90°，
故选：D
| a |
| b |
∴（
| a |
| b |
| a |
| b |
| a |
| b |
∵sinα≠cosα，
∴（
| a |
| b |
| a |
| b |
故向量
| a |
| b |
| a |
| b |
故选：D
点评：本题主要考查了空间向量的坐标运算和数量积的运算，属于基础题
练习册系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
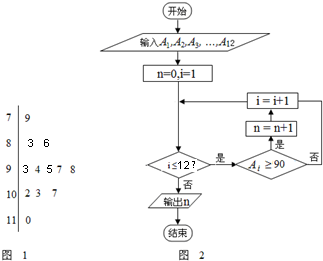图1是某高三学生进入高中三年来的数学考试成绩茎叶图，第1次到12次的考试成绩依次记为A1，A2，…，A12．图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图．那么算法流程图输出的结果是（ ）| A、8 | B、9 | C、10 | D、11 |
曲线y=1-
在点（-1，-1）处的切线方程为（ ）
| 2 |
| x+2 |
| A、y=2x+1 |
| B、y=2x-1 |
| C、y=-2x-3 |
| D、y=-2x-2 |
若过定点M（-1，0）且斜率为k的直线与圆x2+4x+y2-5=0在第一象限内的部分有交点，则k的取值范围是（ ）
A、0＜k＜
| ||
B、-
| ||
C、0＜k＜
| ||
| D、0＜k＜5 |